Question

若不等式（a²-3a+2） x²+（a-1）x+2＞0恒成立，則a的取值范圍    ．

Answer 1

【答案】分析：①討論當a²-3a+2=0時，解得a=1滿足不等式②a²-3a+2≠0時令y=（a²-3a+2）x²+（a-1）x+2．利用一元二次函數圖象討論不等式左邊取值情況．要使對一切實數不等式都成立函數y=（a²-3a+2）x²+（a-1）x+2圖象必須開口向上，且判別式小于0．可解得a范圍③取兩種情況下范圍的并集，可得a最終取值范圍．
解答：（1）當a²-3a+2=0時，即a=1或a=2
顯然當a=1時，不等式變形為 2＞0，對一切實數x都成立
當a=2時，不等式變形為 x+2＞0，不能對一切實數x都成立，故此時a=1滿足
（2）當a²-3a+2≠0時，要使對一切實數不等式都成立必須有開口向上，且判別式小于0
因此有a²-3a+2＞0，（a-1）²-8（a²-3a+2）＜0
解得a＜1或a＞；
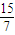
綜合（1）（2）a≤1或a＞．
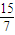
點評：本題考查函數、方程、不等式之間的關系以及一元二次函數圖象
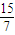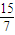