Question

若與球心距離為4的平面截球所得的截面圓的面積是9π，則球的表面積是   

Answer 1

【答案】分析：本題考查的知識點是球的體積和表面積公式，由與球心距離為4的平面截球所得的截面圓的面積是9π，我們易求出截面圓的半徑為3，根據球心距、截面圓半徑、球半徑構成直角三角形，滿足勾股定理，我們易求出該球的半徑，進而求出球的表面積．
解答：解：∵與球心距離為4的平面截球所得的截面圓的面積是9π，
∴d=4時，r=3
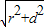
故R==5
∴球的表面積S=4πR²=100π
故答案為：100π
點評：若球的截面圓半徑為r，球心距為d，球半徑為R，則球心距、截面圓半徑、球半徑構成直角三角形，滿足勾股定理，即R²=r²+d²