
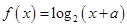 .
.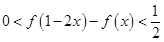 ,當
,當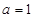 時,求
時,求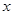 的取值范圍;
的取值范圍;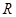 上奇函數
上奇函數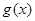 滿足
滿足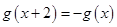 ,且當
,且當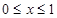 時,
時,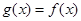 ,求
,求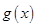 在
在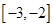 上的反函數
上的反函數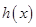 ;
;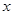 的不等式
的不等式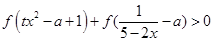 在區間
在區間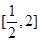 上有解,求實數
上有解,求實數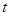 的取值范圍.
的取值范圍.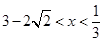 ;(2);(3).
;(2);(3).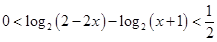 ,即
,即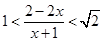 ,但是要注意對數的真數要為正,
,但是要注意對數的真數要為正,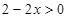 ,
,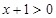 ;(2)
;(2)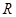 上奇函數
上奇函數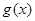 滿足
滿足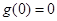 ,可很快求出
,可很快求出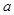 ,要求
,要求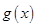 在
在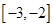 上的反函數,必須求出
上的反函數,必須求出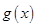 在
在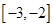 上的解析式,當
上的解析式,當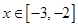 時,
時,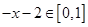 ,故
,故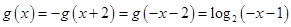 ,當然求反函數還要求出反函數的定義域即原函數的值域;(3)
,當然求反函數還要求出反函數的定義域即原函數的值域;(3)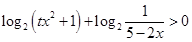 可轉化為
可轉化為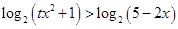 ,這樣利用對數函數的性質得
,這樣利用對數函數的性質得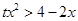 ,變成了整式不等式,問題轉化為不等式
,變成了整式不等式,問題轉化為不等式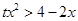 在區間
在區間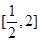 上有解,而這個問題通常采用分離參數法,轉化為求相應函數的值域或最值.
上有解,而這個問題通常采用分離參數法,轉化為求相應函數的值域或最值.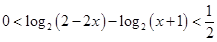 1分
1分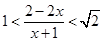 ,
,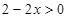 ,
,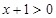 1分
1分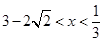 2分
2分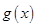 是奇函數,所以
是奇函數,所以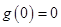 ,得
,得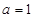 1分
1分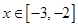 時,
時,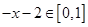
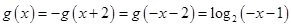 2分
2分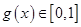 ,
,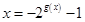 ,所以
,所以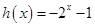
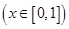 2分
2分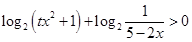 , 1分
, 1分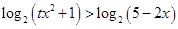 1分
1分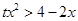 在區間
在區間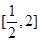 上有解,
上有解,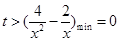 3分
3分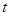 的取值范圍為
的取值范圍為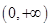 1分
1分

 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com