
 ,其圖象相鄰的兩條對稱軸方程為x=0與
,其圖象相鄰的兩條對稱軸方程為x=0與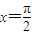 ,則( )
,則( ) 上為單調遞增函數
上為單調遞增函數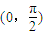 上為單調遞減函數
上為單調遞減函數 ),由題意可得
),由題意可得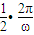 =
= ,解得ω的值,即可確定函數的解析式為f(x)=2sin(2x-
,解得ω的值,即可確定函數的解析式為f(x)=2sin(2x-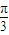 ),由此求得周期,由2kπ-
),由此求得周期,由2kπ-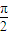 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,求得x的范圍,即可得到函數的增區間,從而得出結論.
,k∈z,求得x的范圍,即可得到函數的增區間,從而得出結論. =2[
=2[ sin(ωx-
sin(ωx-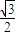 cosωx]=2sin(ωx-
cosωx]=2sin(ωx- ),∴函數的周期為
),∴函數的周期為  .
.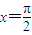 ,可得
,可得  =
= ,解得ω=2,故f(x)=2sin(2x-
,解得ω=2,故f(x)=2sin(2x- ).
). )的周期為
)的周期為 =π.
=π. ≤2x-
≤2x-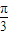 ≤2kπ+
≤2kπ+ ,k∈z,可得kπ-
,k∈z,可得kπ- ≤x≤kπ+
≤x≤kπ+ ,
,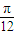 ,kπ+
,kπ+ ],k∈z,故函數在
],k∈z,故函數在 上為單調遞增函數,
上為單調遞增函數,

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2013-2014學年吉林省吉林市普通中學高三(上)開學數學試卷(理科)(解析版) 題型:選擇題
 ,其圖象相鄰的兩條對稱軸方程為x=0與
,其圖象相鄰的兩條對稱軸方程為x=0與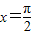 ,則( )
,則( )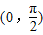 上為單調遞增函數
上為單調遞增函數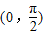 上為單調遞減函數
上為單調遞減函數查看答案和解析>>
科目:高中數學 來源:2013年甘肅省高考數學三模試卷(文科)(解析版) 題型:選擇題
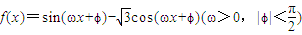 ,其圖象相鄰的兩條對稱軸方程為x=0與
,其圖象相鄰的兩條對稱軸方程為x=0與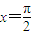 ,則( )
,則( )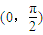 上為單調遞增函數
上為單調遞增函數 上為單調遞減函數
上為單調遞減函數查看答案和解析>>
科目:高中數學 來源:2013年黑龍江省哈爾濱三中高考數學二模試卷(理科)(解析版) 題型:選擇題
 ,其圖象相鄰的兩條對稱軸方程為x=0與
,其圖象相鄰的兩條對稱軸方程為x=0與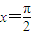 ,則( )
,則( ) 上為單調遞增函數
上為單調遞增函數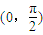 上為單調遞減函數
上為單調遞減函數查看答案和解析>>
科目:高中數學 來源:2014屆吉林省吉林市高三開學摸底考試理科數學試卷(解析版) 題型:選擇題
已知函數 ,其圖象相鄰的兩條對稱軸方程為
,其圖象相鄰的兩條對稱軸方程為 與
與 ,則( )
,則( )
A. 的最小正周期為
的最小正周期為 ,且在
,且在 上為單調遞增函數
上為單調遞增函數
B. 的最小正周期為
的最小正周期為 ,且在
,且在 上為單調遞減函數
上為單調遞減函數
C. 的最小正周期為
的最小正周期為 , 且在
, 且在 上為單調遞增函數
上為單調遞增函數
D. 的最小正周期為
的最小正周期為 , 且在
, 且在 上為單調遞減函數
上為單調遞減函數
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com