Question

已知向量n=(1,0),O是坐標原點,動點P滿足:||比向量在n上的投影多2.

(1)求動點P的軌跡方程;

(2)設B、C是點P的軌跡上不同的兩點,滿足=λ(λ≠0,且λ∈R),在x軸上是否存在點A(m,0)使得⊥?若存在,求出實數m的取值范圍;若不存在,說明理由.

Answer 1

解:(1)設P點的坐標為(x,y),則||=,

向量在n上的投影為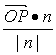=(x,y)·(1,0)=x,                    

所以=x+2.                                                    

化簡得y²=4(x+1),所以動點P的軌跡方程為y²=4(x+1).                        

(2)若兩點B、C滿足條件=λ,得B、O、C三點共線,

設直線BC方程為x=ky,B、C兩點的坐標為(x₁,y₁)、(x₂,y₂),由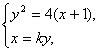得y²-4ky-4=0,

Δ=16k²+16＞0,y₁+y₂=4k,y₁y₂=-4.                                            

又⊥,所以·=0,

即(x₁-m)(x₂-m)+y₁y₂=0,                                                    

x₁x₂-m(x₁+x₂)+m²+y₁y₂=0,

所以(k²+1)y₁y₂-mk(y₁+y₂)+m²=0.

化簡得(4m+4)k²=m²-4,當m=-1時不成立,                                     

當m≠-1時,

有k²=≥0.

解之,得-2≤m＜-1或m≥2.