已知公差不為0的等差數(shù)列
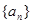
的首項
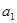
為a
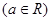
,設(shè)數(shù)列的前n項和為
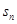
,且
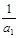
,
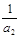
,
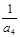
成等比數(shù)列.
(1)求數(shù)列
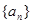
的通項公式及
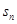
;
(2)記
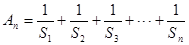
,
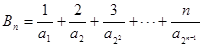
,當(dāng)
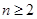
時,計算
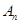
與
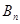
,并比較
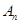
與
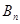
的大小(比較大小只需寫出結(jié)果,不用證明).
(1)
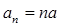
,
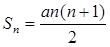
(2)
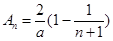
,
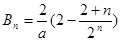
當(dāng)
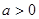
時,
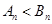
;當(dāng)
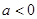
時,
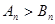
試題分析:(I)解:設(shè)等差數(shù)列
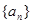
的公差為d,由
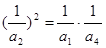
,
得
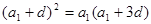
,
因為
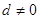
,所以
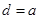
,故
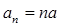
,
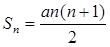
. 4分
(II)解:因為
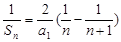
,所以
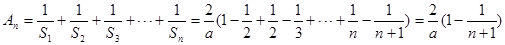
7分
∵
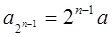
,
∴
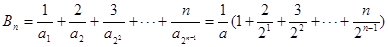
,①
∴
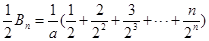
,②
等式①②左右分別相減,得
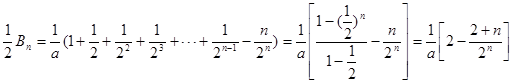
∴
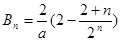
12分
當(dāng)
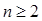
時,
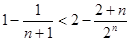
,
所以,當(dāng)
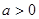
時,
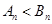
;
當(dāng)
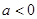
時,
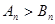
? 14分
點評:第二問數(shù)列求和時用到了裂項相消和錯位相減求和法,這兩種方法是數(shù)列求和題目中常用的方法。裂項相消法一般適用于通項為
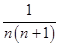
的形式,錯位相減法一般適用于通項為
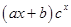
的形式的數(shù)列
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知單調(diào)遞增的等比數(shù)列{a
n}滿足:a
2+a
3+a
4=28,且a
3+2是a
2,a
4的等差中項.
(1)求數(shù)列{a
n}的通項公式;
(2)若

,S
n=b
1+b
2+…+b
n,求使S
n+n·2
n+1>50成立的正整數(shù)n的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
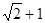
與
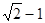
的等比中項等于
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知
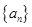
為等比數(shù)列,
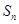
是它的前
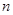
項和.若
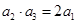
,且
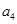
與
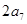
的等差中項為
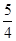
,則
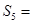
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
已知數(shù)列{an}滿足a1=1,an+an+1="(" 1/4)n(n∈N﹡),Sn=a1+a2•4+a3•42+…+an•4n-1 類比課本中推導(dǎo)等比數(shù)列前n項和公式的方法,可求得5Sn-4nan= .
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
若等比數(shù)列{a
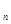
}的前三項和為13,首項為1,則其公比為
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
若△
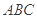
的內(nèi)角
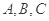
的對邊分別為
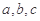
,且
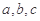
成等比數(shù)列,
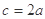
,則
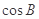
的值為

查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知等比數(shù)列
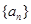
中
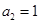
,則其前3項的和
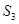
的取值范圍是 ( )
查看答案和解析>>

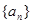 的首項
的首項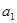 為a
為a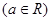 ,設(shè)數(shù)列的前n項和為
,設(shè)數(shù)列的前n項和為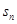 ,且
,且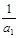 ,
,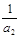 ,
,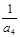 成等比數(shù)列.
成等比數(shù)列.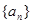 的通項公式及
的通項公式及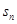 ;
;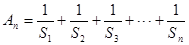 ,
,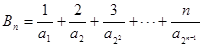 ,當(dāng)
,當(dāng)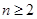 時,計算
時,計算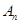 與
與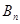 ,并比較
,并比較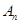 與
與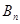 的大小(比較大小只需寫出結(jié)果,不用證明).
的大小(比較大小只需寫出結(jié)果,不用證明). 閱讀快車系列答案
閱讀快車系列答案 ,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的正整數(shù)n的最小值.
,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的正整數(shù)n的最小值.