
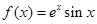 .
.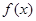 的單調區間;
的單調區間;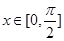 ,
,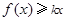 總成立,求實數
總成立,求實數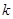 的取值范圍;
的取值范圍;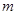 ,使得:當
,使得:當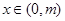 時,不等式
時,不等式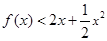 恒成立?請給出結論并說明理由.
恒成立?請給出結論并說明理由.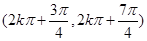
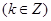 .;(2)
.;(2)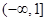 ⑶詳見解析.
⑶詳見解析.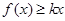 總成立,只需
總成立,只需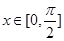 時
時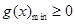 .借助求導,研究
.借助求導,研究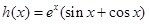 的性質,通過對參數k的討論和單調性的分析探求實數
的性質,通過對參數k的討論和單調性的分析探求實數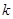 的取值范圍;⑶通過構造函數和等價轉化思想,將問題轉化為
的取值范圍;⑶通過構造函數和等價轉化思想,將問題轉化為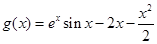 ,要使
,要使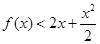 在
在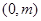 上恒成立,只需
上恒成立,只需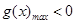 .然后利用求導研究函數的最大值,進而證明結論.
.然后利用求導研究函數的最大值,進而證明結論.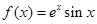 ,
,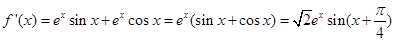 . (2分)
. (2分)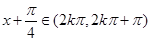 ,即
,即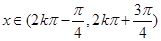 時,
時,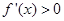 ;
;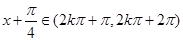 ,即
,即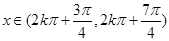 時,
時,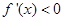 .
.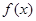 的單調遞增區間為
的單調遞增區間為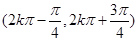
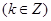 ,
,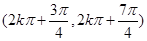
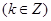 . (4分)
. (4分)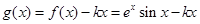 ,要使
,要使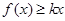 總成立,只需
總成立,只需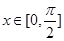 時
時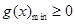 .
.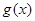 求導得
求導得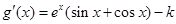 ,
,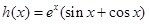 ,則
,則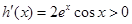 ,(
,(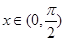 )
)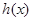 在
在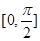 上為增函數,所以
上為增函數,所以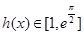 . (6分)
. (6分)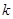 分類討論:
分類討論: 時,
時,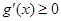 恒成立,所以
恒成立,所以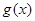 在
在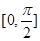 上為增函數,所以
上為增函數,所以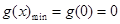 ,即
,即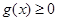 恒成立;
恒成立;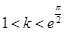 時,
時,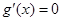 在上有實根
在上有實根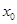 ,因為
,因為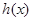 在
在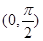 上為增函數,所以當
上為增函數,所以當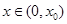 時,
時,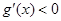 ,所以
,所以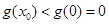 ,不符合題意;
,不符合題意;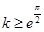 時,
時,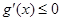 恒成立,所以
恒成立,所以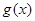 在
在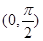 上為減函數,則
上為減函數,則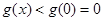 ,不符合題意.
,不符合題意. 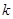 的取值范圍是
的取值范圍是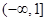 . (9分)
. (9分)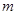 使得當
使得當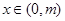 時,不等式
時,不等式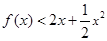 恒成立.
恒成立. 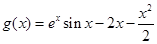 ,要使
,要使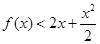 在
在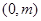 上恒成立,只需
上恒成立,只需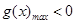 . (10分)
. (10分)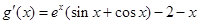 ,且
,且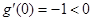 ,
,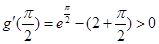 ,所以存在正實數
,所以存在正實數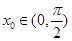 ,使得
,使得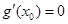 ,
,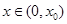 時,
時,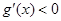 ,
,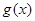 在
在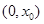 上單調遞減,即當
上單調遞減,即當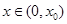 時,
時,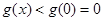 ,所以只需
,所以只需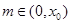 均滿足:當
均滿足:當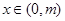 時,
時,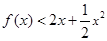 恒成立. (12分)
恒成立. (12分)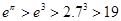 ,
,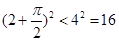 ,所以
,所以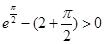


 特高級教師點撥系列答案
特高級教師點撥系列答案科目:高中數學 來源:不詳 題型:填空題
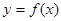 和
和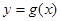 在
在 的圖象如下所示:
的圖象如下所示: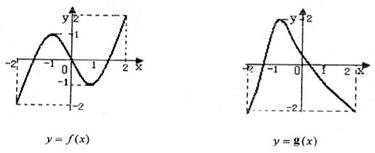
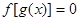 有且僅有6個根 ②方程
有且僅有6個根 ②方程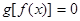 有且僅有3個根
有且僅有3個根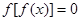 有且僅有5個根 ④方程
有且僅有5個根 ④方程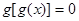 有且僅有4個根
有且僅有4個根查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com