
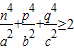 .
.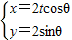 (t為非零常數,θ為參數),在極坐標系(與直角坐標系xOy取相同的長度單位,且以原點O為極點,以x軸正半軸為極軸)中,直線l的方程為
(t為非零常數,θ為參數),在極坐標系(與直角坐標系xOy取相同的長度單位,且以原點O為極點,以x軸正半軸為極軸)中,直線l的方程為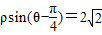 .
.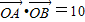 (其中O為坐標原點)?若存在,請求出;否則,請說明理由.
(其中O為坐標原點)?若存在,請求出;否則,請說明理由. ,可得函數的最小值為2.故m=2.
,可得函數的最小值為2.故m=2.

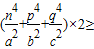 (n2+p2+q2)2=4,故
(n2+p2+q2)2=4,故 .
. .…1分
.…1分 ,化簡得(1+t2)x2+8t2x+12t2=0.
,化簡得(1+t2)x2+8t2x+12t2=0.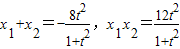 ,…6分
,…6分 =2x1x2+4(x1+x2)+16=10.
=2x1x2+4(x1+x2)+16=10.

 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案科目:高中數學 來源: 題型:
| ||
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| p |
| x |
| 1 |
| e |
| 1 |
| e |
查看答案和解析>>
科目:高中數學 來源: 題型:
|
| 1 |
| an |
| (y-1)2 |
| 4 |
| a |
| b |
| a |
| b |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com