
已知定義在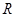 上的函數
上的函數 滿足:
滿足: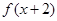 是偶函數,且
是偶函數,且 時的解析式為
時的解析式為 ,則
,則 時
時 的解析式為 ;
的解析式為 ;

解析試題分析:根據函數奇偶性定義,得f(-x+2)=f(x+2).當x<2時,由于4-x>2,將4-x代入已知條件的解析式,可得f(4-x)=,x2-2x-4,而f(4-x)與f(x)相等,由此則不難得到x<2時f(x)的解析式解:∵f(x+2)是偶函數,∴f(-x+2)=f(x+2),設x<2,則4-x>2,可得f(4-x)=(4-x)2-6(4-x)+4=x2-2x-4,,∵f(4-x)=f[2+(2-x)]=f[2-(2-x)]=f(x),∴當x<2時,f(x)=f(4-x)=x2-2x-4,,故答案為:f(x)=x2-2x-4
考點:奇偶性
點評:本題給出定義在R上且圖象關于x=2對稱的函數,在已知x≥2時的解析式情況下求則x<2時f(x)的解析式.著重考查了函數的奇偶性和函數解析式求解的常用方法的知識,屬于基礎題


科目:高中數學 來源: 題型:填空題
關于函數f(x)=4sin(2x+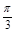 )(x∈R),有下列命題:
)(x∈R),有下列命題:
①由f(x1)=f(x2)=0可得x1-x2必是 的整數倍;
的整數倍;
②y= f(x)的表達式可改寫為y=4cos(2x- );
);
③y= f(x)的圖象關于點(- ,0)對稱;
,0)對稱;
④y= f(x)的圖象關于直線x=- 對稱.
對稱.
其中正確的命題的序號是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com