
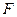 在
在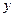 軸上,拋物線上一點
軸上,拋物線上一點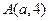 到準(zhǔn)線的距離是
到準(zhǔn)線的距離是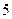 ,過點
,過點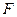 的直線與拋物線交于
的直線與拋物線交于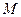 ,
,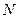 兩點,過
兩點,過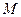 ,
,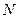 兩點分別作拋物線的切線,這兩條切線的交點為
兩點分別作拋物線的切線,這兩條切線的交點為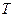 .
.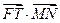 的值;
的值;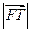 是
是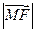 和
和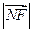 的等比中項.
的等比中項.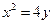 (2)0(3)略
(2)0(3)略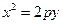
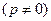 .
.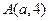 在拋物線上,所以
在拋物線上,所以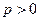 .
.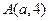 到拋物線準(zhǔn)線的距離是
到拋物線準(zhǔn)線的距離是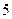 ,所以
,所以 ,可得
,可得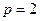 .
.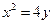 .………………………………………………3分
.………………………………………………3分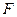 為拋物線的焦點,則
為拋物線的焦點,則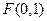 .
.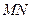 不與
不與 軸垂直,所以設(shè)直線
軸垂直,所以設(shè)直線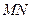 的方程為
的方程為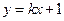 .
. 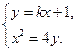 得
得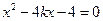 .
.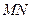 過焦點
過焦點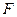 ,所以判別式大于零.
,所以判別式大于零.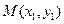 ,
,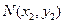 .
. ,
,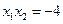 .……………………………………………………6分
.……………………………………………………6分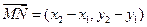
 .
.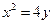 ,所以
,所以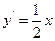 .
.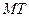 的方程為
的方程為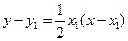 , ①
, ①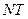 的方程為
的方程為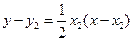 . ②
. ②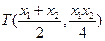 .…………………………………8分
.…………………………………8分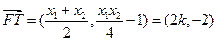 .
.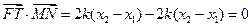 .………………………10分
.………………………10分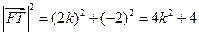 .
.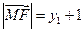 ,
,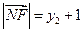 .
.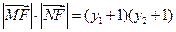
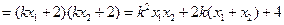
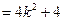 .
.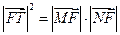 .
.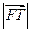 是
是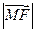 和
和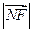 的等比中項.…………………………………………………13分
的等比中項.…………………………………………………13分

科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
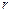 米.市場上,圓柱側(cè)面用料單價為每平方米
米.市場上,圓柱側(cè)面用料單價為每平方米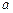 元,圓錐側(cè)面用料單價分別是圓柱側(cè)面用料單價和圓柱底面用料單價的4倍和2倍.設(shè)圓錐母線和底面所成角為
元,圓錐側(cè)面用料單價分別是圓柱側(cè)面用料單價和圓柱底面用料單價的4倍和2倍.設(shè)圓錐母線和底面所成角為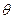 (弧度),總費用為
(弧度),總費用為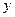 (元).
(元).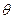 的取值范圍;(2)將
的取值范圍;(2)將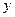 表示成
表示成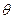 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;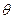 為何值時,總費用
為何值時,總費用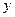 最小?
最小?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
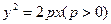 交于
交于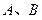 兩點,且
兩點,且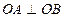 (
(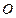 為坐標(biāo)原點),
為坐標(biāo)原點),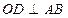 于點
于點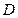 ,點
,點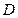 的坐標(biāo)為
的坐標(biāo)為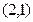
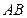 的方程
的方程查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
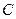 的對稱中心為原點O,焦點在
的對稱中心為原點O,焦點在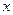 軸上,離心率為
軸上,離心率為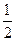 ,且點(1,
,且點(1,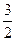 )在該橢圓上.
)在該橢圓上.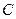 的方程;
的方程;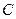 的左焦點
的左焦點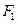 的直線
的直線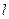 與橢圓
與橢圓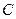 相交于
相交于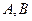 兩點,若
兩點,若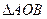 的面積為
的面積為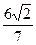 ,求圓心在原點O且與直線
,求圓心在原點O且與直線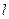 相切的圓的方
相切的圓的方 程.
程. 查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
 的公共左右頂點,P、Q分別位于橢圓和雙曲線上且不同于A、B的兩點,設(shè)直線AP、BP、AQ、BQ的斜率分別為k1、k2、k3、k4且k1+k2+k3+k4=0。
的公共左右頂點,P、Q分別位于橢圓和雙曲線上且不同于A、B的兩點,設(shè)直線AP、BP、AQ、BQ的斜率分別為k1、k2、k3、k4且k1+k2+k3+k4=0。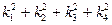 的值。
的值。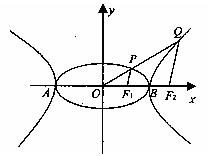
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
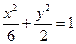 的焦點,P是曲線
的焦點,P是曲線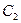 :
: 與C1的一個交點,
與C1的一個交點,| A. | B.1 | C. | D.2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
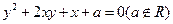 to the y-axis is
to the y-axis is  then the velue of a is
then the velue of a isA.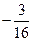 | B.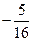 | C.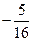 or or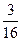 | D.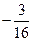 or or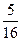 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
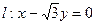 與曲線
與曲線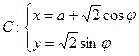
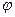 為參數(shù),
為參數(shù),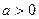 )有兩個公共點A,B,且|AB|=2,則實數(shù)a的值為 ;在此條件下,以直角坐標(biāo)系的原點為極點,x軸正方向為極軸建立坐標(biāo)系,則曲線C的極坐標(biāo)方程為 .
)有兩個公共點A,B,且|AB|=2,則實數(shù)a的值為 ;在此條件下,以直角坐標(biāo)系的原點為極點,x軸正方向為極軸建立坐標(biāo)系,則曲線C的極坐標(biāo)方程為 .查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com