
已知函數f(x)= (b<0)的值域是[1,3],
(b<0)的值域是[1,3],
(1)求b、c的值;
(2)判斷函數F(x)=lgf(x),當x∈[-1,1]時的單調性,并證明你的結論;
(3)若t∈R,求證:lg ≤F(|t-
≤F(|t- |-|t+
|-|t+ |)≤lg
|)≤lg .
.
(1)解:設y=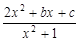 ,則(y-2)x2-bx+y-c=0 ①
,則(y-2)x2-bx+y-c=0 ①
∵x∈R,∴①的判別式Δ≥0,即 b2-4(y-2)(y-c)≥0,
即4y2-4(2+c)y+8c-b2≤0 ②
由條件知,不等式②的解集是[1,3]
∴1,3是方程4y2-4(2+c)y+8c-b2=0的兩根
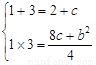 ∴c=2,b=-2,b=2(舍)
∴c=2,b=-2,b=2(舍)
(2)任取x1,x2∈[-1,1],且x2>x1,則x2-x1>0,且
(x2-x1)(1-x1x2)>0,
∴f(x2)-f(x1)=-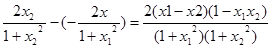 >0,
>0,
∴f(x2)>f(x1),lgf(x2)>lgf(x1),即F(x2)>F(x1)
∴F(x)為減函數.
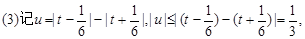
即-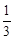 ≤u≤
≤u≤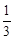 ,根據F(x)的單調性知
,根據F(x)的單調性知
F(-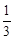 )≤F(u)≤F(
)≤F(u)≤F(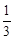 ),∴lg
),∴lg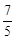 ≤F(|t-
≤F(|t-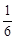 |-|t+
|-|t+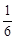 |)≤lg
|)≤lg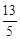 對任意實數t 成立.
對任意實數t 成立.
【解析】(1)由已知中函數的值域是[1,3],利用判別式法,我們可以構造出一個關于b,c的方程組,解方程組即可得到b,c的值;
(2)由(1)的結論我們易給出函數F(x)=lgf(x)的解析式,利用作差法,我們可以判斷出F(x1)與F(x2)的大小,結合函數單調性的定義,我們易判斷出函數F(x)=lgf(x)在[-1,1]上的單調性.
(3)根據函數的單調性得到不等式的證明,。


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:高中數學 來源: 題型:
|
| 1 |
| π |
查看答案和解析>>
科目:高中數學 來源: 題型:
 已知函數f(x)=
已知函數f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| x-1 | x+a |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com