
在數列 中,
中, ,
, ,其中
,其中 .
.
(1)設 ,求數列
,求數列 的通項公式;
的通項公式;
(2)記數列 的前
的前 項和為
項和為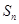 ,試比較
,試比較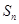 與
與 的大小.
的大小.
 手拉手全優練考卷系列答案
手拉手全優練考卷系列答案科目:高中數學 來源: 題型:
|
| 1 |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
在數列![]() 中,
中,![]() ,若
,若![]() (
(![]() 為常數),則稱
為常數),則稱![]() 為“等差比數列”. 下列是對“等差比數列”的判斷:
為“等差比數列”. 下列是對“等差比數列”的判斷:
①![]() 不可能為0 ②等差數列一定是等差比數列
不可能為0 ②等差數列一定是等差比數列
③等比數列一定是等差比數列 ④等差比數列中可以有無數項為0
其中正確的判斷的序號是: 。
查看答案和解析>>
科目:高中數學 來源:2010年上海市高二上學期期中考試數學卷 題型:填空題
在數列 中,如果存在非零常數
中,如果存在非零常數 ,使得
,使得 對于任意非零正整數
對于任意非零正整數 均成立,那么就稱數列
均成立,那么就稱數列 為周期數列,其中
為周期數列,其中 叫做數列
叫做數列 的周期.已知周期數列
的周期.已知周期數列 滿足
滿足 (
( )且
)且 ,
,
 ,當
,當 的周期最小時,該數列前2005項和是 .
的周期最小時,該數列前2005項和是 .
查看答案和解析>>
科目:高中數學 來源:2010-2011年湖北省高一期中考試數學理卷 題型:填空題
.定義:在數列 中,若
中,若 ,(
,(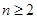 ,
,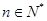 ,
,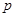 為常數),則稱
為常數),則稱 為“等方差數列”.下列是對“等方差數列”的有關判斷:
為“等方差數列”.下列是對“等方差數列”的有關判斷:
①若 是“等方差數列”,則數列
是“等方差數列”,則數列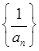 是等差數列;
是等差數列;
② 是“等方差數列”;
是“等方差數列”;
③若 是“等方差數列”,則數列
是“等方差數列”,則數列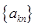 (
( ,
, 為常數)也是“等方差數列”;
為常數)也是“等方差數列”;
④若 既是“等方差數列”,又是等差數列,則該數列是常數數列.
既是“等方差數列”,又是等差數列,則該數列是常數數列.
其中正確的命題為 .(寫出所有正確命題的序號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com