中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情
若函數f（x）=（x+a）（bx+2a）（常數a、b∈R）是偶函數，且它的值域為（-∞，4]，求該函數的解析式．
分析：由f（x）=（x+a）（bx+2a）是偶函數，知f（-x）=（-x+a）（-bx+2a）=f（x）=（x+a）（bx+2a），故2ax+abx=0，a=0或2+b=0．由此能求出f（x）的解析式．
解答：解：∵f（x）=（x+a）（bx+2a）是偶函數，
∴f（-x）=（-x+a）（-bx+2a）=f（x）=（x+a）（bx+2a），
∴bx2-2ax-abx+2a2=bx2+2ax+abx+2a2，
∴2ax+abx=0，即ax（2+b）=0恒成立，
∴a=0或2+b=0．
若a=0，則f（x）=bx2，若b＞0，值域是y≥0，b＜0，值域是y≤0，都不是（-∞，4]，
所以a≠0，故b+2=0，
∴b=-2，
所以f（x）=-2x2+2a2，
∵-2x2≤0，
所以值域是f（x）≤2a2，
∴2a2=4，
即f（x）=-2x2+4．
點評：本題考查二次函數的性質和應用，是基礎題．解題時要認真審題，仔細解答，注意合理地進行等價轉化．
練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

設函數f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函數y=f（x）圖象上的點到直線x-y-3=0距離的最小值為
2
，求a的值；
（2）關于x的不等式（x-1）2＞f（x）的解集中的整數恰有3個，求實數a的取值范圍；
（3）對于函數f（x）與g（x）定義域上的任意實數x，若存在常數k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，則稱直線y=kx+m為函數f（x）與g（x）的“分界線”．設a=
2
2
，b=e，試探究f（x）與g（x）是否存在“分界線”？若存在，求出“分界線”的方程；若不存在，請說明理由．

查看答案和解析>>

科目：高中數學 來源： 題型：

若函數 f（x）＝a x (a＞0，a≠1 ) 的部分對應值如表：

x

－2

0

f（x）

0.592

1

則不等  式f－1（│x│＜0）的解集是        （）

A. {x│－1＜x＜1}                  B. {x│x＜－1或x＞1}         

C. {x│0＜x＜1}                    D. {x│－1＜x＜0或0＜x＜1}

查看答案和解析>>

科目：高中數學 來源： 題型：單選題

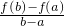若函數f（x）對于任意x∈[a，b]，恒有|f（x）-f（a）-數學公式（x-a）|≤T（T為常數）成立，則稱函數f（x）在[a，b]上具有“T級線性逼近”．下列函數中：
①f（x）=2x+1；
②f（x）=x2；
③f（x）=數學公式；
④f（x）=x3．
則在區間[1，2]上具有“數學公式級線性逼近”的函數的個數為


  1. A.
    1
  2. B.
    2
  3. C.
    3
  4. D.
    4

查看答案和解析>>

科目：高中數學 來源：徐州模擬 題型：解答題

設函數f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函數y=f（x）圖象上的點到直線x-y-3=0距離的最小值為2
2
，求a的值；
（2）關于x的不等式（x-1）2＞f（x）的解集中的整數恰有3個，求實數a的取值范圍；
（3）對于函數f（x）與g（x）定義域上的任意實數x，若存在常數k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，則稱直線y=kx+m為函數f（x）與g（x）的“分界線”．設a=
2
2
，b=e，試探究f（x）與g（x）是否存在“分界線”？若存在，求出“分界線”的方程；若不存在，請說明理由．

查看答案和解析>>

科目：高中數學 來源：2013年福建省寧德市高三質量檢查數學試卷（理科）（解析版） 題型：選擇題

若函數f（x）對于任意x∈[a，b]，恒有|f（x）-f（a）-（x-a）|≤T（T為常數）成立，則稱函數f（x）在[a，b]上具有“T級線性逼近”．下列函數中：
①f（x）=2x+1；
②f（x）=x2；
③f（x）=；
④f（x）=x3．
則在區間[1，2]上具有“級線性逼近”的函數的個數為（ ）
A．1
B．2
C．3
D．4

查看答案和解析>>

同步練習冊答案