
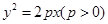 上的點M分別向C的準線和x軸作垂線,兩條垂線及C的準線和x軸圍成邊長為4的正方形,點M在第一象限.
上的點M分別向C的準線和x軸作垂線,兩條垂線及C的準線和x軸圍成邊長為4的正方形,點M在第一象限.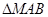 面積的最大值.
面積的最大值. .
.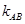 中得到直線AB的斜率,設出直線AB的方程,利用M點在直線AB上方得到b的范圍,令直線與拋物線方程聯立,圖形有2個交點,所以方程的
中得到直線AB的斜率,設出直線AB的方程,利用M點在直線AB上方得到b的范圍,令直線與拋物線方程聯立,圖形有2個交點,所以方程的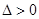 進一步縮小b的范圍,
進一步縮小b的范圍,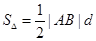 ,而
,而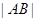 用兩點間距離公式轉化,d是M到直線AB的距離,再利用導數求面積的最大值.
用兩點間距離公式轉化,d是M到直線AB的距離,再利用導數求面積的最大值.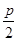 ,依題意M(4-
,依題意M(4-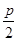 ,4),
,4),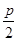 ),解得p=4.
),解得p=4.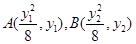 .
.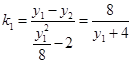 ,同理直線MB的斜率
,同理直線MB的斜率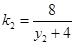 .
. ,整理得y1+y2=-8.
,整理得y1+y2=-8.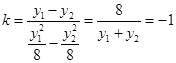 . 6分
. 6分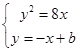 得y2+8y-8b=0.
得y2+8y-8b=0.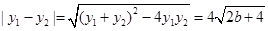 ,
,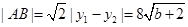 .
.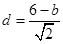 ,則△MAB的面積
,則△MAB的面積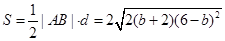 .
. 時,f¢(x)>0;當
時,f¢(x)>0;當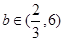 時,f¢(x)<0.
時,f¢(x)<0.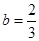 時,f(b)最大,從而S取得最大值
時,f(b)最大,從而S取得最大值 . 12分
. 12分

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:不詳 題型:填空題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
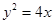 的焦點為F,過點P(2,0)的直線交拋物線于A,B兩點,直線AF,BF分別于拋物線交于點C,D.設直線AB,CD的斜率分別為
的焦點為F,過點P(2,0)的直線交拋物線于A,B兩點,直線AF,BF分別于拋物線交于點C,D.設直線AB,CD的斜率分別為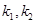 ,則
,則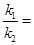 ( )
( )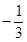 B.
B.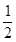 C.1 D.2
C.1 D.2查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com