Question

已知f(x)=x³+bx²+cx+d在(-∞,0)上是增函數,在［0,2］上是減函數,且方程f(x)=0有三個根,它們分別為α、2、β.

(1)求c的值；(2)求證：f(1)≥2;(3)求|α-β|的取值范圍.

Answer 1

解:（1）f′(x)=3x²+2bx+c.∵f(x)在（-∞,0）上是增函數，在［0，2］上是減函數，∴x=0時，f(x)取得極大值，∴f′(0)=0.即c=0,從而f(x)=x³+bx²+d.

(2)由題設f(2)=0,即d=-4(b+2),則f(1)=1+b+d=-7-3b.又

f′(x)=3x²+2bx,令f′(x)=0,得x₁=0或x₂=-b.

∵f(x)在［0，2］上是減函數，從而-b≥2,即b≤-3,∴f(1)=-7-3b≥2.

(3)∵α、2、β是f(x)=0的三個根，從而

f(x)=(x-α)(x-2)(x-β)=x³-(2+α+β)x²+(2a+2β+αβ)x-2αβ,

    于是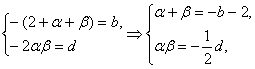

∴|α-β|=

∵b≤-3,∴|α-β|≥3.

說明:本題涉及到了三次方程的根與系數的關系：設一元三次方程ax³+bx²+cx+d=0的三個根為x₁、x₂、x₃,則ax³+bx²+cx+d=a(x-x₁)(x-x₂)(x-x₃)展開即可得到根x₁、x₂、x₃與系數a、b、c、d的關系.