Question

(08年龍巖一中模擬文)（12分）

如圖，已知直線與拋物線相切于點P(2，1)，且與x軸交于點A，O為坐標(biāo)原點，定點B的坐標(biāo)為（2，0）.

（Ⅰ）若動點M滿足，求點M的軌跡C；

（Ⅱ）若過點B的直線（斜率不等于零）與（Ⅰ）中的軌跡C交于不同的兩點E、F（E在B、F之間），試求△OBE與△OBF面積之比的取值范圍.

Answer 1

解析：（Ⅰ）由，  

∴直線的斜率為， ………………………1分

故的方程為，

∴點A坐標(biāo)為（1，0） ……………………………………… 2分

設(shè)    則，

由得

整理，得 ………………………………………………4分

∴動點M的軌跡C為以原點為中心，焦點在x軸上，長軸長為，短軸長為2的橢圓 …………………………………………………………………………………… 5分

 

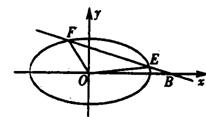
（Ⅱ）如圖，由題意知直線的斜率存在且不為零，設(shè)方程為y=k(x－2)(k≠0)①

將①代入，整理，得

，

由△>0得0<k²<.   設(shè)E(x₁，y₁)，F(xiàn)(x₂，y₂)

則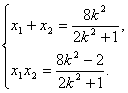 ②     …………………………………………7分

令，

由此可得

由②知

.

∴△OBE與△OBF面積之比的取值范圍是（3－2，1）.………………12分