
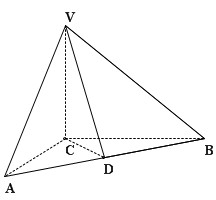
如圖,在三棱錐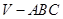 中,
中,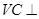 底面
底面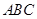 ,
, 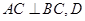 為
為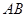 的中點,
的中點,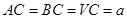 .
.
(1)求證: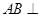 平面
平面 ;
;
(2)求點 到平面
到平面 的距離。
的距離。
(1)證明過程詳見解析;(2)點 到平面
到平面 的距離為
的距離為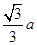 .
.
解析試題分析:本題以三棱錐為幾何背景考查線面垂直的判斷和點到面的距離的求法,可以運用傳統(tǒng)幾何法求解,突出考查空間想象能力和計算能力.第一問,先利用線面垂直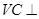 平面
平面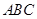 ,得到線線垂直
,得到線線垂直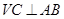 ,由等腰三角形,得
,由等腰三角形,得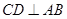 ,由上述兩個條件得
,由上述兩個條件得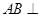 平面
平面 ;第二問,利用第一問可得面
;第二問,利用第一問可得面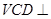 面
面 ,利用面面垂直的性質(zhì),得
,利用面面垂直的性質(zhì),得 到
到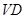 的距離即為
的距離即為 到面
到面 的距離,在直角三角形
的距離,在直角三角形 中,用等面積法表示
中,用等面積法表示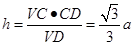 .法二:第二問,等體積法求點面距離,
.法二:第二問,等體積法求點面距離, ,即
,即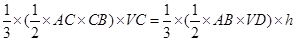 ,得
,得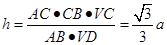 .
.
試題解析:(1)因為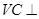 平面
平面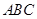 ,
, 平面
平面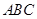 ,
,
所以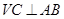 2分
2分
又因為在 中,
中,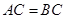 ,
,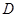 為
為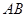 的中點,
的中點,
所以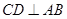 4分
4分
又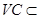 平面
平面 ,
,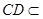 平面
平面 ,且
,且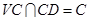 ,
,
所以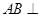 平面
平面 6分
6分
(2)法一:因為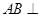 平面
平面 且
且 平面
平面
所以平面
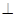 平面
平面 , 8分
, 8分
又因為平面
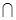 平面
平面
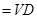 ,
,
所以點 到
到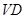 的距離
的距離 即為點
即為點 到平面
到平面 的距離, 10分
的距離, 10分
在直角三角形 中,由
中,由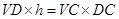 11分
11分
得 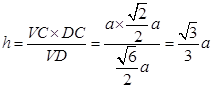 13分
13分
所以點 到平面
到平面 的距離為
的距離為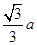 . 14分
. 14分
法二:設點 到平面
到平面 的距離為
的距離為 , 據(jù)
, 據(jù)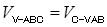 8分
8分
即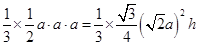 ,得
,得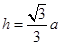 13分
13分
所以點 到平面
到平面 的距離為
的距離為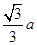 . 14分
. 14分
考點:1.線面垂直的判定定理;2.面面垂直的性質(zhì);3.等體


 導學全程練創(chuàng)優(yōu)訓練系列答案
導學全程練創(chuàng)優(yōu)訓練系列答案科目:高中數(shù)學 來源: 題型:解答題
如圖,邊長為2的正方形ABCD,E,F分別是AB,BC的中點,將△AED,△DCF分別沿DE,DF折起,使A,C兩點重合于 .
.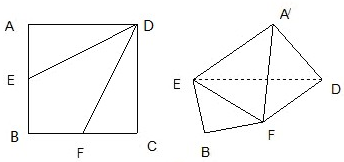
(1)求證: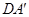 ⊥EF;
⊥EF;
(2)求二面角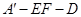 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
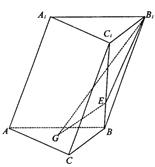
如圖,在斜三棱柱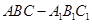 中,側(cè)面
中,側(cè)面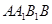 ⊥底面
⊥底面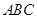 ,側(cè)棱
,側(cè)棱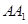 與底面
與底面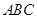 成
成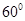 的角,
的角,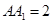 .底面
.底面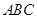 是邊長為2的正三角形,其重心為
是邊長為2的正三角形,其重心為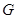 點,
點,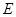 是線段
是線段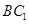 上一點,且
上一點,且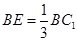 .
.
(Ⅰ)求證: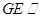 //側(cè)面
//側(cè)面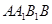 ;
;
(Ⅱ)求平面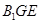 與底面
與底面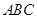 所成銳二面角的正切值.
所成銳二面角的正切值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
如圖,在四棱錐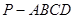 中,底面ABCD是正方形,側(cè)棱
中,底面ABCD是正方形,側(cè)棱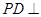 底面ABCD,
底面ABCD,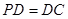 ,E是PC的中點.
,E是PC的中點.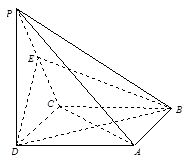
(Ⅰ)證明 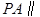 平面EDB;
平面EDB;
(Ⅱ)求EB與底面ABCD所成的角的正切值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
如圖,直三棱柱ABC-A1B1C1中,D,E分別是AB,BB1的中點,AA1=AC=CB=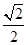 AB.
AB.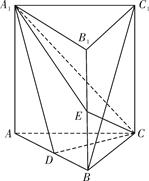
(Ⅰ)證明:BC1∥平面A1CD;
(Ⅱ)求二面角D-A1C-E的正弦值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com