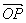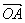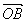Question

設(shè)橢圓方程為x²+=1,過點(diǎn)M（0,1）的直線l交橢圓于點(diǎn)A、B，O是坐標(biāo)原點(diǎn)，點(diǎn)P滿足=（+），點(diǎn)N的坐標(biāo)為（，）.當(dāng)l繞點(diǎn)M旋轉(zhuǎn)時(shí)，求：

（1）動(dòng)點(diǎn)P的軌跡方程；

（2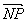）||的最小值與最大值.

Answer 1

思路解析：（1）設(shè)出l的斜率k，根據(jù)題設(shè)條件列出方程組，解得P點(diǎn)的坐標(biāo)（用k表示），消去參數(shù)k即得.（2）則可化為區(qū)間上二次函數(shù)的最值問題.

（1）解法一：直線l過點(diǎn)M（0,1），設(shè)其斜率為k，則l的方程為y=kx+1.

設(shè)A(x₁,y₁)、B（x₂,y₂）,由題設(shè)可得點(diǎn)A、B的坐標(biāo)（x₁,y₁）、（x₂,y₂）是方程組

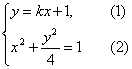
的解.

將（1）代入（2）并化簡(jiǎn),得（4+k²）x²+2kx-3=0,

所以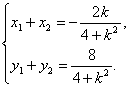

于是=（+）

=(,)=(,).

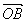設(shè)點(diǎn)P的坐標(biāo)為（x,y），則

消去參數(shù)k,得4x²+y²-y=0.                                                       （3）

當(dāng)k不存在時(shí)，A、B中點(diǎn)為坐標(biāo)原點(diǎn)（0，0），也滿足方程（3），所以點(diǎn)P的軌跡方程為4x²+y²-y=0.

解法二：設(shè)點(diǎn)P的坐標(biāo)為（x,y），因A（x₁,y₁）、B(x₂,y₂)在橢圓上，

所以x₁²+=1,④,x₂²+=1.                                           ⑤

④-⑤,得x₁²-x₂²+(y₁²-y₂²)=0,

所以（x₁-x₂）(x₁+x₂)+(y₁-y₂)(y₁+y₂)=0.

當(dāng)x₁≠x₂時(shí)，有x₁+x₂+(y₁+y₂)·=0,                      ⑥

并且                                                         ⑦

將⑦代入⑥并整理,得4x²+y²-y=0.                                              ⑧

當(dāng)x₁=x₂時(shí)，點(diǎn)A、B的坐標(biāo)為（0，2）、（0，-2），這時(shí)點(diǎn)P的坐標(biāo)為（0，0）,也滿足⑧,所以點(diǎn)P的軌跡方程為+=1.

(2)解：由點(diǎn)P的軌跡方程知x²≤，即-≤x≤.

所以|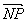|²=(x-)²+(y-)²=(x-)²+-4x²

=-3(x+)²+,

故當(dāng)x=時(shí)，||取得最小值，最小值為；

當(dāng)x=-時(shí)，||取得最大值，最大值為.