
 ,且矩陣M對應的變換將點(-1,2)變換成
,且矩陣M對應的變換將點(-1,2)變換成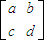 ,則
,則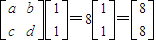 ,故
,故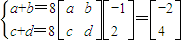 ,由此得到
,由此得到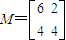 ,從而得到矩陣M的另一個特征值及對應的一個特征向量e2的坐標之間的關系.
,從而得到矩陣M的另一個特征值及對應的一個特征向量e2的坐標之間的關系.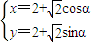 (α為參數) (6分)
(α為參數) (6分)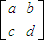 ,則
,則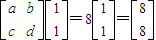 ,
, ,
,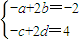
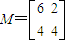 .(10分)
.(10分)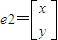 ,
,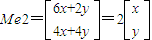 ,
,

 53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源: 題型:
 在A,B,C,D四小題中只能選做2題,每題10分,共計20分.
在A,B,C,D四小題中只能選做2題,每題10分,共計20分.| x2 |
| 4 |
| y2 |
| 9 |
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
| π |
| 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com