.如圖所示,已知正四棱錐S—ABCD中,底面邊長為a,側(cè)棱長為
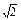
a.
(1)求它的外接球的體積;
(2)求它的內(nèi)切球的表面積.
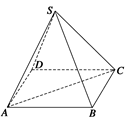
(1)V
球=
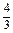

R
3=
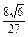

a
3(2)V
棱錐=
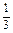
S
底h=
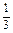
a
2×

a=

(1)設(shè)外接球的半徑為R,球心為O,則OA=OC=OS,所以O(shè)為△SAC的外心,
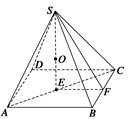
即△SAC的外接圓半徑就是球的半徑.
∵AB=BC=a,∴AC=
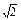
a.
∵SA=SC=AC=
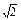
a,∴△SAC為正三角形.
由正弦定理得2R=

,
因此,R=
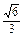
a,V
球=
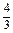

R
3=
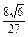

a
3.
(2)設(shè)內(nèi)切球半徑為r,作SE⊥底面ABCD于E,
作SF⊥BC于F,連接EF,
則有SF=

=
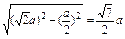
.
S
△SBC=

BC·SF=

a×
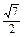
a=
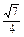
a
2.
S
棱錐全=4S
△SBC+S
底=(
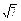
+1)a
2.
又SE=
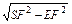
=
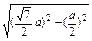
=
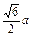
,
∴V
棱錐=
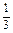
S
底h=
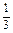
a
2×

a=

.
∴r=
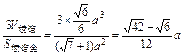
,
S
球=4

r
2=


a
2.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
一個直棱柱的對角線長是9 cm和15 cm,高是5 cm,若它的底面是菱形,則這個直棱柱的側(cè)面積是( )
| A.160 cm2 | B.320 cm2 | C. cm2 cm2 | D. cm2 cm2 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
若棱臺的上下底面面積分別為
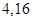
,高為
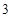
,則該棱臺的體積為( ).
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
若四面體各棱的長是1或2,且該四面體不是正四面體,則其體積的值是_______.(只需寫出一個可能的值)
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
一個正四棱臺的斜高為12,側(cè)棱長為13,側(cè)面積為720,求它的體積.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
底面為平行四邊形的四棱柱各棱長均為4,在由頂點P出發(fā)的三條棱上分別取PA=1,PB=2,PC=3,則
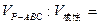
__________
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
如果圓臺的母線與底面成60°角,那么這個圓臺的側(cè)面積與軸截面面積的比為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
如圖,在上、下底面對應(yīng)邊的比為1∶2的三棱臺中,過上底面一邊作一個平行于對棱的平面A
1B
1EF,這個平面分三棱臺成兩部分的體積之比為( )

查看答案和解析>>

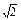 a.
a.
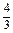
 R3=
R3=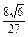
 a3(2)V棱錐=
a3(2)V棱錐=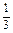 S底h=
S底h=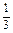 a2×
a2× a=
a=

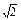 a.
a.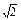 a,∴△SAC為正三角形.
a,∴△SAC為正三角形. ,
,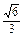 a,V球=
a,V球=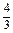
 R3=
R3=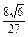
 a3.
a3.
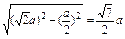 .
. BC·SF=
BC·SF= a×
a×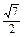 a=
a=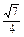 a2.
a2.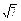 +1)a2.
+1)a2.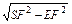 =
=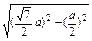 =
=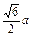 ,
, S底h=
S底h= a2×
a2× a=
a= .
.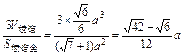 ,
, r2=
r2=
 a2.
a2.

 習(xí)題精選系列答案
習(xí)題精選系列答案 cm2
cm2 cm2
cm2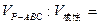 __________
__________