用分析法證明:若

,則

.
解:要證原不等式,只需證
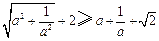
.

,

兩邊均大于零.
因此只需證

,
只需證

,
只需證

,即證
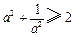
,而
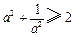
顯然成立,

原不等式成立.
19.若下列方程:

,

,

,至少有一個方程有實根,試求實數(shù)

的取值范圍.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:填空題
用反證法證明命題 “對任意

、
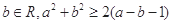
”,正確的反設為
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
實數(shù)
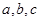
滿足

,則

的值
| A.一定是正數(shù) | B.一定是負數(shù) | C.可能是0 | D.正、負不確定 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
設f(x)=ax
2+bx+c(a≠0),若函數(shù)f(x+1)與f(x)的圖象關于y軸對稱.求證:f(x+
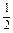
)為偶函數(shù).
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知數(shù)列{a
n}中,a
1=1,且a
n=
an-1+2n•3n-2(n≥2,n∈N*).
(1)求a
2,a
3,a
4的值;
(2)寫出數(shù)列{a
n}的通項公式,并用數(shù)學歸納法證明.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
.已知

為等比數(shù)列,

,則

.若

為等差數(shù)列,

,則

的類似結論為 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若

,且

恒成立,則

的最大值為( )
| A.2 | B.3  | C.4 | D.5 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
分析法又稱執(zhí)果索因法,若用分析法證明:“設
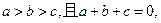
求證
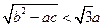
”索的因應是( )
A
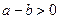
B
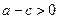
C
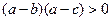
D
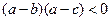
查看答案和解析>>

 ,則
,則 .
.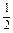 )為偶函數(shù).
)為偶函數(shù).