
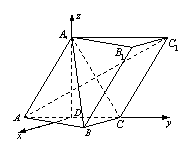
(08年鷹潭市一模理)(12分)已知斜三棱柱![]() ,
,![]() ,
,![]() ,
,![]() 在底面
在底面![]() 上的射影恰為
上的射影恰為![]() 的中點
的中點![]() ,又知
,又知![]() .
.
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求![]() 到平面
到平面![]() 的距離;
的距離;
(Ⅲ)求二面角![]() 的大小.
的大小.

解析:解法![]() :(Ⅰ)∵
:(Ⅰ)∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() , 得
, 得![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() .…………………4分
.…………………4分
(Ⅱ)∵![]() ,四邊形
,四邊形![]() 為菱形,故
為菱形,故![]() ,
,
又![]() 為
為![]() 中點,知∴
中點,知∴![]() .取
.取![]() 中點
中點![]() ,則
,則
![]() 平面
平面![]() ,從而面
,從而面![]() 面
面![]() ,…………6分
,…………6分
過![]() 作
作![]() 于
于![]() ,則
,則![]() 面
面![]() ,在
,在![]() 中,
中,![]() ,故
,故![]() ,即
,即![]() 到平面
到平面![]() 的距離為
的距離為![]() .…………………8分
.…………………8分
(Ⅲ)過![]() 作
作![]() 于
于![]() ,連
,連![]() ,則
,則![]() ,從而
,從而![]() 為二面角
為二面角![]() 的平面角,在
的平面角,在![]() 中,
中,![]() ,∴
,∴![]() ,…………10分
,…………10分
在![]() 中,
中,![]() ,故二面角
,故二面角![]() 的大小為
的大小為![]() .
.
…………………12分
解法![]() :(Ⅰ)如圖,取
:(Ⅰ)如圖,取![]() 的中點
的中點![]() ,則
,則![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
又![]() 平面
平面![]() ,以
,以![]() 為
為![]() 軸建立空間坐標系, …………1分
軸建立空間坐標系, …………1分
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,由
,由![]() ,知
,知![]() ,
,
又![]() ,從而
,從而![]() 平面
平面![]() .…………………4分
.…………………4分
(Ⅱ)由![]() ,得
,得![]() .設平面
.設平面![]() 的法向量
的法向量
為![]() ,
,![]() ,
,![]() ,
,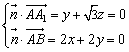 ,
,
設![]() ,則
,則![]() .…………6分
.…………6分
∴點![]() 到平面
到平面![]() 的距離
的距離![]() .…………………8分
.…………………8分
(Ⅲ)設面![]() 的法向量為
的法向量為![]() ,
,![]() ,
,![]() ,
,
∴ .…………10分
.…………10分
設![]() ,則
,則![]() ,故
,故![]() ,根據法向量的方向
,根據法向量的方向
可知二面角![]() 的大小為
的大小為![]() .…………………12分
.…………………12分



科目:高中數學 來源: 題型:
(08年鷹潭市一模理)(14分)已知函數![]() 滿足
滿足![]() ,
,![]() ,
,![]() ;且使
;且使![]() 成立的實數
成立的實數![]() 只有一個。
只有一個。
(Ⅰ)求函數![]() 的表達式;
的表達式;
(Ⅱ)若數列![]() 滿足
滿足![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,證明數列
,證明數列![]() 是等比數列,并求出
是等比數列,并求出![]() 的通項公式;
的通項公式;
(Ⅲ)在(Ⅱ)的條件下,如果![]() ,
,
![]() ,證明:
,證明:![]() ,
,![]() 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年鷹潭市一模理) (12分)在一次語文測試中,有一道我國四大文學名著《水滸傳》、《三國演義》、《西游記》、《紅樓夢》與它們的作者的連線題,已知連對一個得2分,連錯一個不得分.
(Ⅰ)求該同學得分的分布列;
(Ⅱ)求該同學得分的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年鷹潭市一模理) 已知![]() 為第二象限角,且
為第二象限角,且![]() ,那么
,那么![]() 的取值范圍是( )
的取值范圍是( )
A. ( -1 ,0 ) B. ( 1 , ![]() ) C. ( -1 ,1 ) D. ( -
) C. ( -1 ,1 ) D. ( -![]() ,-1 )
,-1 )
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com