
如圖,F1,F2是離心率為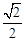 的橢圓C:
的橢圓C: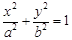 (a>b>0)的左、右焦點,直線
(a>b>0)的左、右焦點,直線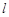 :x=-
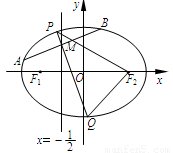
:x=-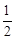 將線段F1F2分成兩段,其長度之比為1 : 3.設A,B是C上的兩個動點,線段AB的中垂線與C交于P,Q兩點,線段AB的中點M在直線l上.
將線段F1F2分成兩段,其長度之比為1 : 3.設A,B是C上的兩個動點,線段AB的中垂線與C交于P,Q兩點,線段AB的中點M在直線l上.
(Ⅰ) 求橢圓C的方程;
(Ⅱ) 求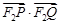 的取值范圍.
的取值范圍.
(Ⅰ)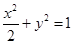 ;(Ⅱ)
;(Ⅱ)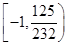 .
.
【解析】
試題分析:(Ⅰ)根據題中的已知條件列有關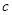 的方程,求出
的方程,求出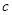 ,然后根據離心率求出
,然后根據離心率求出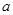 ,最后再根據
,最后再根據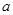 、
、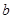 、
、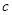 三者之間的關系求出
三者之間的關系求出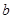 的值,從而確定橢圓
的值,從而確定橢圓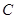 的方程;(Ⅱ)先設點
的方程;(Ⅱ)先設點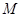 的坐標
的坐標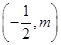 ,然后根據已知條件將直線
,然后根據已知條件將直線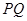 的方程用
的方程用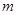 進行表示,再聯立直線
進行表示,再聯立直線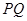 與橢圓
與橢圓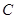 的方程,結合韋達定理將
的方程,結合韋達定理將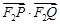 表示為含
表示為含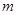 為代數式,然后再利用不等式的性質求出
為代數式,然后再利用不等式的性質求出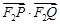 的取值范圍.
的取值范圍.
試題解析:(Ⅰ)設F2(c,0),則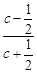 =
=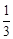 ,所以c=1.
,所以c=1.
因為離心率e=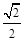 ,所以a=
,所以a=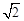 .
.
所以橢圓C的方程為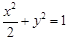 .
.
(Ⅱ) 當直線AB垂直于x軸時,直線AB方程為x=-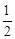 ,此時P(
,此時P(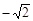 ,0)、Q(
,0)、Q(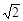 ,0),
,0),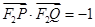 .
.
當直線AB不垂直于x軸時,設直線AB的斜率為k,M(-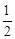 ,m) (m≠0),A(x1,y1),B(x2,y2).
,m) (m≠0),A(x1,y1),B(x2,y2).
由 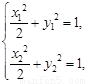 得(x1+x2)+2(y1+y2)
得(x1+x2)+2(y1+y2) =0,
=0,
則-1+4mk=0,故k=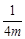 .
.
此時,直線PQ斜率為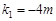 ,PQ的直線方程為
,PQ的直線方程為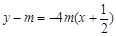 .即
.即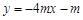 .
.
聯立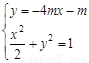 消去y,整理得
消去y,整理得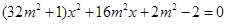 .
.
所以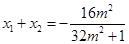 ,
,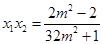 .
.
于是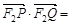 (x1-1)(x2-1)+y1y2
(x1-1)(x2-1)+y1y2
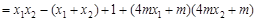

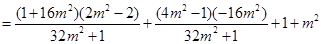
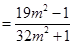 .
.
令t=1+32m2,1<t<29,則 .
.
又1<t<29,所以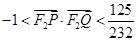 .
.
綜上,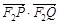 的取值范圍為
的取值范圍為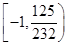 .
.
考點:橢圓的方程、平面向量的數量積、韋達定理


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案科目:高中數學 來源: 題型:
 如圖,F1,F2是離心率為
如圖,F1,F2是離心率為
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•浙江模擬)如圖,F1,F2是離心率為
(2013•浙江模擬)如圖,F1,F2是離心率為
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| F2P |
| F2Q |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年浙江省臨海市高三第三次模擬理科數學試卷(解析版) 題型:解答題
如圖,F1,F2是離心率為 的橢圓C:
的橢圓C: (a>b>0)的左、右焦點,直線:x=-
(a>b>0)的左、右焦點,直線:x=- 將線段F1F2分成兩段,其長度之比為1 : 3.設A,B是C上的兩個動點,線段AB的中垂線與C交于P,Q兩點,線段AB的中點M在直線l上.
將線段F1F2分成兩段,其長度之比為1 : 3.設A,B是C上的兩個動點,線段AB的中垂線與C交于P,Q兩點,線段AB的中點M在直線l上.

(Ⅰ) 求橢圓C的方程;
(Ⅱ) 求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江西南昌10所省高三第二次模擬突破沖刺理科數學(一)(解析版) 題型:解答題
如圖,F1,F2是離心率為 的橢圓
的橢圓
C: (a>b>0)的左、右焦點,直線
(a>b>0)的左、右焦點,直線 :x=-
:x=- 將線段F1F2分成兩段,其長度之比為1 : 3.設A,B是C上的兩個動點,線段AB的中點M在直線l上,線段AB的中垂線與C交于P,Q兩點.
將線段F1F2分成兩段,其長度之比為1 : 3.設A,B是C上的兩個動點,線段AB的中點M在直線l上,線段AB的中垂線與C交于P,Q兩點.

(Ⅰ) 求橢圓C的方程;
(Ⅱ) 是否存在點M,使以PQ為直徑的圓經過點F2,若存在,求出M點坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年浙江省高三高考模擬測試理科數學試卷(解析版) 題型:解答題
如圖,F1,F2是離心率為 的橢圓C:
的橢圓C: (a>b>0)的左、右焦點,直線
(a>b>0)的左、右焦點,直線 :x=-
:x=- 將線段F1F2分成兩段,其長度之比為1 : 3.設A,B是C上的兩個動點,線段AB的中垂線與C交于P,Q兩點,線段AB的中點M在直線l上.
將線段F1F2分成兩段,其長度之比為1 : 3.設A,B是C上的兩個動點,線段AB的中垂線與C交于P,Q兩點,線段AB的中點M在直線l上.

(Ⅰ) 求橢圓C的方程;
(Ⅱ) 求 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com