
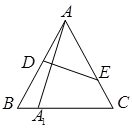
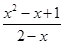 (0≤x≤1), AD=
(0≤x≤1), AD=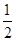 ·
·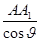 =
=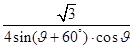 θ∈[0º,60º]
θ∈[0º,60º] -3 當且僅當
-3 當且僅當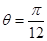 時取得最小值.
時取得最小值.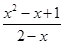 (0≤x≤1),
(0≤x≤1), 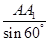 =
=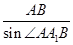 =
=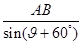 ∴AA1=
∴AA1=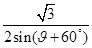 ,
,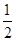 ·
·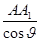 =
=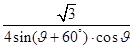 θ∈[0º,60º]
θ∈[0º,60º]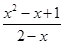 (0≤x≤1),令t=2-x∈[1,2]∴y=
(0≤x≤1),令t=2-x∈[1,2]∴y=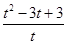 =t+
=t+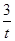 -3≥2
-3≥2 -3
-3 ,即x=2-
,即x=2- 時等號成立.AD長度的最小值為2
時等號成立.AD長度的最小值為2 -3.
-3.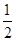 ·
·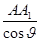 =
=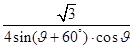 θ∈[0º,60º]
θ∈[0º,60º] cos2θ=sin2θ+
cos2θ=sin2θ+ (1+cos2θ)=sin2θ+
(1+cos2θ)=sin2θ+ cos2θ+
cos2θ+ =2sin(2θ+60º)+
=2sin(2θ+60º)+
 ,2+
,2+ ]∴AD≥
]∴AD≥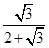 =
= (2-
(2- )=2
)=2 -3∴AD長度的最小值為2
-3∴AD長度的最小值為2 -3 當且僅當
-3 當且僅當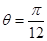 時取得最小值.
時取得最小值.

 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應(yīng)用題卡系列答案
口算與應(yīng)用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
 為銳角△
為銳角△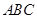 的內(nèi)心,且
的內(nèi)心,且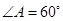 ,點
,點 為內(nèi)切圓
為內(nèi)切圓 與邊
與邊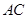 的切點,過點
的切點,過點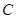 作直線
作直線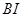 的垂線,垂足為
的垂線,垂足為 .
.
 ;
; 的值.
的值.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
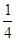 圓周,C點是弧BE上的任意一點, △ABD是等邊三角形,則四邊形ABCD的周長p的取值范圍是
圓周,C點是弧BE上的任意一點, △ABD是等邊三角形,則四邊形ABCD的周長p的取值范圍是 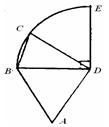
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
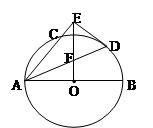
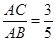 ,求
,求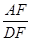 的值.
的值.查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com