
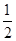 PD.
PD.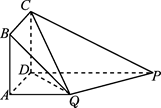
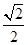 PD,則PQ⊥QD.
PD,則PQ⊥QD. a3.
a3.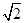 a,△DCQ的面積為
a,△DCQ的面積為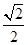 a2,
a2, a3.
a3.

科目:高中數學 來源:不詳 題型:單選題
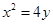 和直線
和直線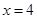 ,
,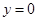 所圍成的平面圖形,繞
所圍成的平面圖形,繞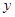 軸旋轉一周所得到的旋轉體為
軸旋轉一周所得到的旋轉體為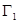 ;由同時滿足
;由同時滿足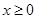 ,
,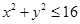 ,
,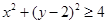 ,
,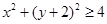 的點
的點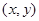 構成的平面圖形,繞
構成的平面圖形,繞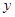 軸旋轉一周所得到的旋轉體為
軸旋轉一周所得到的旋轉體為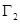 .根據祖暅原理等知識,通過考察
.根據祖暅原理等知識,通過考察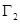 可以得到
可以得到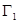 的體積為
的體積為A. | B. | C. | D. |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
A.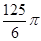 | B.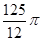 | C.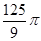 | D.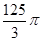 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com