
 .
. 在區間(-2,0)內恰有兩個零點,求a的取值范圍;
在區間(-2,0)內恰有兩個零點,求a的取值范圍; 在區間[t,t+3]上的最大值.
在區間[t,t+3]上的最大值.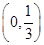 (2)
(2)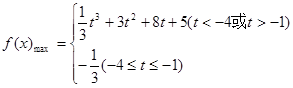
 求導,獲得導函數
求導,獲得導函數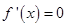 的根與大于0小于0的解集,獲得函數
的根與大于0小于0的解集,獲得函數 的單調區間和極值點,極值.進而確定函數
的單調區間和極值點,極值.進而確定函數 在區間
在區間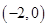 上的單調性,再利用數形結合的思想與零點存在性定理的知識可以得到函數在
上的單調性,再利用數形結合的思想與零點存在性定理的知識可以得到函數在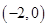 上要有兩個零點,需要
上要有兩個零點,需要 滿足
滿足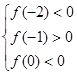 即可,解不等式即可求出
即可,解不等式即可求出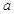 的取值范圍.
的取值范圍.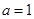 ,則利用(1)可以得到
,則利用(1)可以得到 的單調性以及極值點,極值.要得到函數
的單調性以及極值點,極值.要得到函數 在含參數的區間
在含參數的區間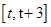 上的最大值,我們需要討論
上的最大值,我們需要討論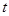 的范圍得到函數
的范圍得到函數 的在區間
的在區間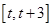 上的單調性進而得到
上的單調性進而得到 在該區間上的最大值,為此分三種情況分別為
在該區間上的最大值,為此分三種情況分別為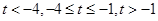 ,依次確定單調性得到最大值即可.
,依次確定單調性得到最大值即可.
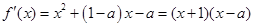 , (1分)
, (1分)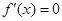 ,解得
,解得 (2分)
(2分)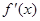 ,
, 的變化情況如下表:
的變化情況如下表: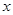 | 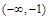 | 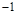 | 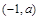 | 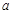 | 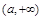 |
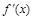 | 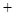 | 0 | — | 0 | 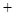 |
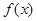 | ↗ | 極大值 | ↘ | 極小值 | ↗ |
 的單調遞增區間為(-∞,-1),(a,+∞);單調遞減區間為(-1,a);(4分)
的單調遞增區間為(-∞,-1),(a,+∞);單調遞減區間為(-1,a);(4分) 在區間(-2,-1)內單調遞增,在區間(-1,0)內單調遞減,要使函數
在區間(-2,-1)內單調遞增,在區間(-1,0)內單調遞減,要使函數 在區間
在區間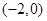 內恰有兩個零點,當且僅當
內恰有兩個零點,當且僅當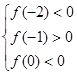 , (5分)
, (5分)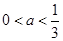 , 所以a的取值范圍是(0,
, 所以a的取值范圍是(0,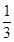 ). (6分)
). (6分)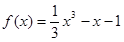 . 由(1)可知,函數
. 由(1)可知,函數 的單調遞增區間為(-∞,-1),(1,+∞);單調遞減區間為(-1,1);
的單調遞增區間為(-∞,-1),(1,+∞);單調遞減區間為(-1,1);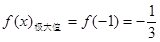 . (7分)
. (7分) 在區間[t,t+3]上單調遞增,所以
在區間[t,t+3]上單調遞增,所以 在區間[t,t+3]上的最大值為
在區間[t,t+3]上的最大值為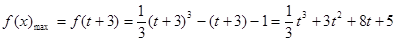 ; (9分)
; (9分)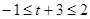 ,即
,即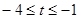 時,
時, 在區間
在區間 上單調遞增,在區間[-1,1]上單調遞減,在區間[1,2]上單調遞增,且
上單調遞增,在區間[-1,1]上單調遞減,在區間[1,2]上單調遞增,且 ,所以
,所以 在區間
在區間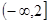 上的最大值為
上的最大值為 . (10分)
. (10分)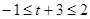 ,即
,即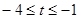 時,有[t,t+3]Ì
時,有[t,t+3]Ì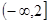 ,-1Î[t,t+3],所以
,-1Î[t,t+3],所以 在
在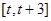 上的最大值為
上的最大值為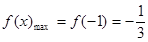 ; (11分)
; (11分) 在區間
在區間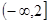 上的最大值為
上的最大值為 .
.  在區間(1,+∞)上單調遞增,所以
在區間(1,+∞)上單調遞增,所以 ,
, 在
在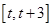 上的最大值為
上的最大值為 . (13分)
. (13分) 在[t,t+3]上的最大值
在[t,t+3]上的最大值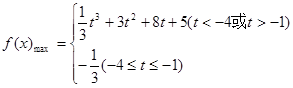 . (14分)
. (14分)

 口算題天天練系列答案
口算題天天練系列答案科目:高中數學 來源:不詳 題型:解答題
 .
. 時,求函數
時,求函數 的單調區間;
的單調區間; 在區間
在區間 上為減函數,求實數
上為減函數,求實數 的取值范圍;
的取值范圍; 時,不等式
時,不等式 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 x3+
x3+ x2+2ax.
x2+2ax. ,+∞)上存在單調遞增區間,求a的取值范圍.
,+∞)上存在單調遞增區間,求a的取值范圍. ,求f(x)在該區間上的最大值.
,求f(x)在該區間上的最大值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com