
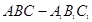 中,
中,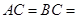
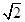 ,且
,且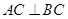 ,點
,點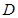 是
是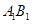 中點.
中點.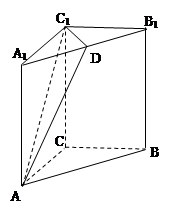
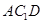 ⊥平面
⊥平面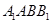 ;
;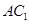 與平面
與平面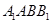 所成角的正弦值為
所成角的正弦值為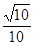 ,
,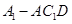 的體積.
的體積. 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
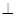 平面ABCD,且AD= 2PA,E、F、G、H分別是線段PA、PD、CD、BC的中點.
平面ABCD,且AD= 2PA,E、F、G、H分別是線段PA、PD、CD、BC的中點.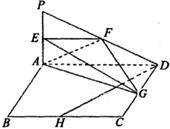
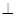 平面AEG.
平面AEG.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
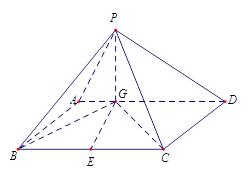
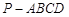 中,底面
中,底面 是平行四邊形,
是平行四邊形,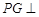 平面
平面 ,垂足為
,垂足為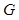 ,
,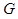 在
在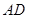 上且
上且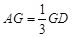 ,
,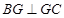 ,
,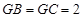 ,
,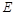 是
是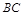 的中點,四面體
的中點,四面體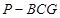 的體積為
的體積為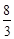 .
.
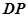 到平面
到平面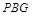 所成角的正弦值;
所成角的正弦值;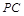 上是否存在一點
上是否存在一點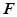 ,使
,使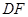
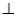
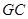 ,若存在,確定點
,若存在,確定點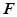 的位置,若不存在,說明理由.
的位置,若不存在,說明理由.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
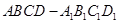 中,點
中,點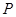 在側面
在側面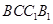 及其邊界上運動,并且總是保持
及其邊界上運動,并且總是保持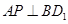 ,則動點
,則動點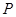 的軌跡是 ( )
的軌跡是 ( )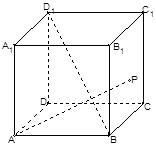
A.線段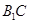 |
B.線段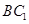 |
C.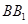 中點與 中點與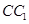 中點連成的線段 中點連成的線段 |
D.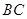 中點與 中點與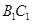 中點連成的線段 中點連成的線段 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
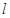 上有無數(shù)個點不在平面
上有無數(shù)個點不在平面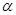 內(nèi),則
內(nèi),則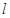 ∥
∥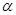 .
.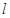 與平面
與平面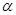 平行,則
平行,則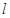 與平面
與平面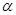 內(nèi)的任意一條直線都平行.
內(nèi)的任意一條直線都平行.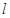 與平面
與平面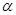 平行,則
平行,則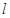 與平面
與平面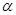 內(nèi)的任意一條直線都沒有公共點.
內(nèi)的任意一條直線都沒有公共點.| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
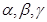 是三個不同的平面,上述命題中真命題的是
是三個不同的平面,上述命題中真命題的是| A.若a⊥c,b⊥c,則a∥b或a⊥b |
B.若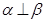 , ,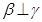 ,則 ,則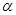 ∥ ∥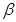 ; ; |
C.若a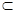 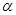 ,b ,b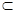 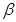 ,c ,c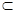 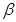 ,a⊥b, a⊥c,則 ,a⊥b, a⊥c,則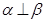 ; ; |
D.若a⊥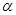 , b , b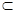 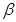 ,a∥b,則 ,a∥b,則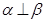 |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com