Question

已知A(3,0)及雙曲線E:-=1,若雙曲線E的右支上的點Q到點B(m,0)(m≥3)距離的最小值為|AB|.?

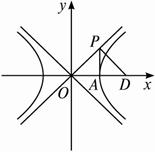
(1)求m的取值范圍,并指出當m變化時點B的軌跡G.

(2)軌跡G上是否存在一點D,它在直線y=x上的射影為P,使得·=·?若存在,試指出雙曲線E的右焦點F分向量所成的比；若不存在,請說明理由.

                 

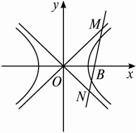
(3)當m為定值時,過軌跡G上的點B(m,0)作一條直線l與雙曲線E的右支交于不同的兩點,且與直線y=x,y=-x分別交于M,N兩點,求△MON周長的最小值.

Answer 1

解:(1)設M(x,y),則x≥3且y²=x²-16,

那么點M到點B的距離d==.?

設f(x)=d²,則f(x)=(x-)²+M²-16(x≥3).                                 ?

當≤3即M≤時,f(x)是［3,+∞)上的增函數,所以當x=3時,f(x)取最小值M-3=|AB|;

當＞3即M＞時,f()=＜m-3.                               ?

由上述可得,當且僅當3≤M≤時,M到B的距離為|AB|.?

所以點B的軌跡是一條線段AN,其中N(,0),即軌跡G為線段AN.          ?

(2)設存在D,令P(3T,4T),則D(T,0),?

于是=(3T-3,4T), =(T,0),?

∴·=25T²-25T.?

又·=0,     ∴25T²-25T=0.?

∴T=0或T=1.                                                                                           ?

當T=0時,D為(0,0)不滿足題意;?

當T=1時,D為(,0)在軌跡G上,?

∴存在D滿足題意.此時D(,0),F(5,0),?

有=(2,0),=(,0),=.?

從而F分所成的比為λ=.                                                         ?

(3)設M(3s,4s),N(3T,-4T),?

因為直線l與雙曲線E的右支有兩個交點,所以s＞0,T＞0.?

由M,B,N共線知=,即=.                                        ?

而(s+T)=()(s+T)=2+≥2+2=4.?

所以s+T≥,當且僅當s=T=時取等號.                                               ?

△OMN的周長L=|OM|+|ON|+|MN|=5s+5T+?

=5(s+T)+?

≥9(s+T)≥6M.?

所以,當s=T=時,△OMN的周長最小為6M.