
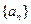 的前
的前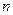 項和為
項和為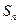 ,對一切
,對一切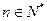 ,點
,點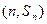 在函數
在函數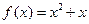 的圖象上.
的圖象上.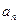 的表達式;
的表達式;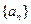 依次按1項、2項、3項、4項循環地分為(
依次按1項、2項、3項、4項循環地分為(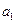 ),(
),(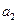 ,
,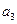 ),(
),(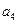 ,
,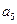 ,
,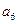 ),(
),(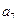 ,
,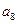 ,
,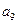 ,
,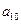 );(
);(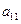 ),(
),(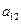 ,
,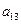 ),(
),(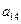 ,
,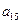 ,
,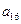 ),(
),(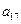 ,
,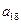 ,
,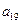 ,
,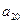 );(
);(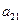 ),…,分別計算各個括號內所有項之和,并設由這些和按原來括號的前后順序構成的數列為
),…,分別計算各個括號內所有項之和,并設由這些和按原來括號的前后順序構成的數列為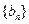 ,求
,求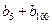 的值;
的值;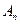 為數列
為數列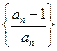 的前
的前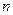 項積,是否存在實數
項積,是否存在實數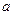 ,使得不等式
,使得不等式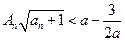 對一切
對一切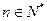 都成立?若存在,求出
都成立?若存在,求出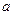 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.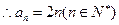 ,2010,
,2010,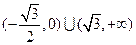
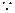 點
點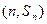 在函數
在函數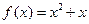 上,
上,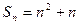 .
. 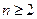 時,
時,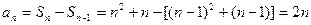
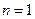 時,
時,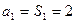 滿足
滿足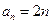 .
.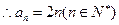 .
. 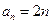 (
(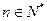 ),所以數列
),所以數列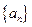 依次按1項、2項、3項、4項循環地分為(2),(4,6),(8,10,12),(14,16,18,20);(22),(24,26),(28,30,32),(34,36,38,40);(42),…. 每一次循環記為一組.由于每一個循環含有4個括號, 故
依次按1項、2項、3項、4項循環地分為(2),(4,6),(8,10,12),(14,16,18,20);(22),(24,26),(28,30,32),(34,36,38,40);(42),…. 每一次循環記為一組.由于每一個循環含有4個括號, 故 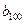 是第25組中第4個括號內各數之和.由分組規律知,由各組第4個括號中所有第1個數組成的數列是等差數列,且公差為20. 同理,由各組第4個括號中所有第2個數、所有第3個數、所有第4個數分別組成的數列也都是等差數列,且公差均為20. 故各組第4個括號中各數之和構成等差數列,且公差為80. 注意到第一組中第4個括號內各數之和是68,
是第25組中第4個括號內各數之和.由分組規律知,由各組第4個括號中所有第1個數組成的數列是等差數列,且公差為20. 同理,由各組第4個括號中所有第2個數、所有第3個數、所有第4個數分別組成的數列也都是等差數列,且公差均為20. 故各組第4個括號中各數之和構成等差數列,且公差為80. 注意到第一組中第4個括號內各數之和是68,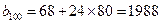 .又
.又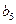 =22,所以
=22,所以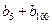 ="2010."
="2010." 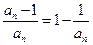 ,故
,故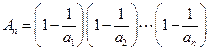 ,
, .
.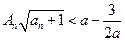 對一切
對一切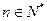 都成立,即
都成立,即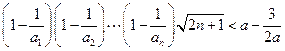 對一切
對一切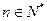 都成立
都成立 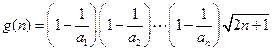 ,則只需
,則只需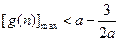 即可.
即可.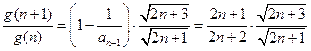
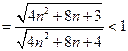 ,
,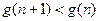 ,故
,故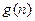 是單調遞減,于是
是單調遞減,于是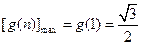
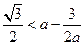 ,即
,即 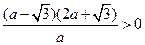 ,解得
,解得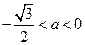 ,或
,或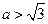 .
.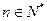 都成立的實數
都成立的實數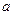 存在,
存在,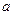 的取值范圍是
的取值范圍是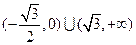 .
. 

 中考解讀考點精練系列答案
中考解讀考點精練系列答案 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案科目:高中數學 來源:不詳 題型:解答題
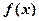 ,存在實數
,存在實數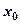 ,使得對于任意實數
,使得對于任意實數 ,總有
,總有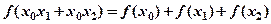 恒成立。
恒成立。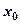 的值;(Ⅱ)若
的值;(Ⅱ)若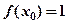 ,且對任意
,且對任意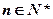 ,有
,有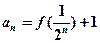 ,求{an}的通項公式;
,求{an}的通項公式;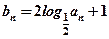 ,將數列{bn}的項重新組合成新數列
,將數列{bn}的項重新組合成新數列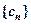 ,具體法則如下:
,具體法則如下: ,……,求證:
,……,求證: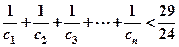 。
。查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
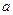
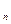 },(n∈N
},(n∈N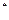 )是等差數列,則有數列b
)是等差數列,則有數列b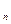 =
=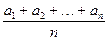 (n∈N
(n∈N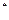 )也是等差數列,類比上述性質,相應地:若數列{c
)也是等差數列,類比上述性質,相應地:若數列{c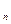 }是等比數列,且c
}是等比數列,且c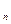 >0(n∈N
>0(n∈N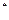 ),則有d
),則有d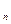 =_______ (n∈N
=_______ (n∈N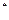 )也是等比數列.
)也是等比數列.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com