
設f(x)=2x3+ax2+bx+1的導數為f′(x),若函數y=f′(x)的圖象關于直線x=- 對稱,且f′(1)=0.
對稱,且f′(1)=0.
(1)求實數a,b的值;
(2)求函數f(x)的極值.
(1)a=3. b=-12.(2)函數f(x)在x1=-2處取得極大值f(-2)=21,在x2=1處取得極小值f(1)=-6.
解析試題分析:(1)先求出 的導函數f′(x)=
的導函數f′(x)=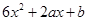 ,由函數y=f′(x)的圖象關于直線x=-
,由函數y=f′(x)的圖象關于直線x=- 對稱及二次函數的性質求出
對稱及二次函數的性質求出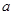 ,再由f′(1)=0求出
,再由f′(1)=0求出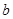 ;(2)將(1)中的
;(2)將(1)中的 值代入導函數中,利用導函數研究函數
值代入導函數中,利用導函數研究函數 的單調性,根據單調性及極值的有關知識求出
的單調性,根據單調性及極值的有關知識求出 的極值.
的極值.
試題解析:(1)由題知f′(x)= 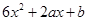 ,
,
由函數y=f′(x)的圖象關于直線x=- 對稱得,
對稱得,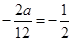 ,解得a=3,
,解得a=3,
由f′(1)=0即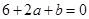 解得b=-12. 所以a=3. b=-12. 6分
解得b=-12. 所以a=3. b=-12. 6分
(2)由(1)知a=3, b=-12,所以f′(x)= 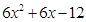 =
=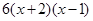 ,
,
當 <-2或
<-2或 >1時,
>1時,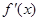 >0,當-2<
>0,當-2< <1時,
<1時,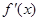 <0,所以
<0,所以 單調增區間為(-
單調增區間為(-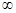 ,-2),(1,+
,-2),(1,+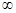 ),單調減區間為(-2,1),所以函數f(x)在x1=-2處取得極大值f(-2)=21,
),單調減區間為(-2,1),所以函數f(x)在x1=-2處取得極大值f(-2)=21,
在x2=1處取得極小值f(1)=-6. 12分
考點:常見函數的導數,導數的運算法則,二次函數的對稱性,函數的極值


 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學教材完全解讀系列答案
小學教材完全解讀系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com