已知函數f(x)=ax3+bx2+cx+d在(-∞,1)上單調遞減,在(1,3)上單調遞增在(3,+∞)上單調遞減,且函數圖象在(2,f(2))處的切線與直線5x+y=0垂直.
(Ⅰ)求實數a、b、c的值;
(Ⅱ)設函數f(x)=0有三個不相等的實數根,求d的取值范圍.
【答案】
分析:(Ⅰ)對函數求導可得,f′(x)=3ax
2+2bx+c,由題意可得

,所以f′(1)=2a+2b+c=0,f′(3)=27a+6b+c=0.聯立可求a,b,c
(Ⅱ)由(Ⅰ)可得f(x),由x=1和x=3分別是函數f(x)的極小值點和極大值點,且當x取負值且絕對值足夠大時,y取正值,當x時正值且足夠大時,y取負值,則方程f(x)=0有三個不相等的實數根的充要條件為
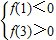
,代入可求
解答:解:(Ⅰ)對函數求導可得,f′(x)=3ax
2+2bx+c,
∵函數圖象在(2,f(2))處的切線與直線5x+y=0垂直,
∴
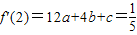
.①
由已知可知,1和3為方程f′(x)=0的兩根,所以f′(1)=2a+2b+c=0,②
f′(3)=27a+6b+c=0.③
由①、②、③解得

,
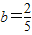
,
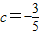
.(6分)
(Ⅱ)由(Ⅰ)得
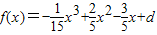
,
∵x=1和x=3分別是函數f(x)的極小值點和極大值點,且當x取負值且絕對值足夠大時,y取正值,當x時正值且足夠大時,y取負值.(8分)
所以方程f(x)=0有三個不相等的實數根的充要條件為

即
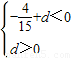
所以d的取值范圍為

.(12分)
點評:本題主要考查了導數的幾何意義:導數在某點處的導數即為改點的切線的斜率,導數的極值存在的條件的應用及利用函數與方程的相互轉化求解參數的范圍,屬于導數知識的綜合應用.

 ,所以f′(1)=2a+2b+c=0,f′(3)=27a+6b+c=0.聯立可求a,b,c
,所以f′(1)=2a+2b+c=0,f′(3)=27a+6b+c=0.聯立可求a,b,c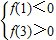 ,代入可求
,代入可求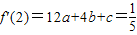 .①
.① ,
,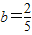 ,
,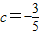 .(6分)
.(6分)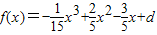 ,
, 即
即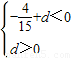
 .(12分)
.(12分)
