
 ������
������ ��
�� �����ھ��
�����ھ�� ������׃�Q���õ��ĈD�ε���e.
������׃�Q���õ��ĈD�ε���e. С�W(xu��)��ĩ��(bi��o)��(zh��n)ԇ��ϵ�д�
С�W(xu��)��ĩ��(bi��o)��(zh��n)ԇ��ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
 ��������c(di��n)��
��������c(di��n)�� �ęE�A���̣�
�ęE�A���̣� ��������10���p��
��������10���p�� �����̡�
�����̡��鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
 ���Ƅ�(d��ng)��������OPA��픽ǡ�OPA��120�㣨O��P��A��형r(sh��)�?l��)������У������c(di��n)P��܉�E����
���Ƅ�(d��ng)��������OPA��픽ǡ�OPA��120�㣨O��P��A��형r(sh��)�?l��)������У������c(di��n)P��܉�E����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
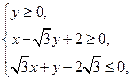 ����ӈAC�cx�S�����c(di��n)A1��A2���E�AC1�Ծ���A1A2���L(zh��ng)�S���x����
����ӈAC�cx�S�����c(di��n)A1��A2���E�AC1�Ծ���A1A2���L(zh��ng)�S���x����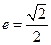 ��
�� �c
�c �S�����S�����c(di��n)D��
�S�����S�����c(di��n)D�� �c(di��n)������(bi��o)ԭ�c(di��n)��
�c(di��n)������(bi��o)ԭ�c(di��n)�� ���c(di��n)��
���c(di��n)�� ����(w��n)�Ƿ����ֱ��
����(w��n)�Ƿ����ֱ�� �c�E�A
�c�E�A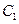 ����
����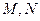 ���c(di��n)����
���c(di��n)����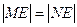 �������ڣ����ֱ��
�������ڣ����ֱ��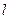 �c
�c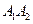 �A��
�A��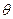 ������ֵ��ȡֵ�������������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
������ֵ��ȡֵ�������������ڣ�Ո(q��ng)�f(shu��)�����ɣ��鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
 ����������
����������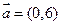 ��ƽ��׃�Q������
��ƽ��׃�Q������ ��������
�������� ����sϵ��(sh��)
����sϵ��(sh��) ����
���� �S����s׃�Q���ٰ���sϵ��(sh��)3����
�S����s׃�Q���ٰ���sϵ��(sh��)3���� �S����s׃�Q�õ�����
�S����s׃�Q�õ�����
 ��
�� ���̣�
���̣� ��
�� ��һ�c(di��n)��
��һ�c(di��n)�� ��
�� ������һ�c(di��n)����
������һ�c(di��n)���� �c����
�c���� ����
���� �����c(di��n)����
�����c(di��n)���� �����ֵ����(du��)��(y��ng)��
�����ֵ����(du��)��(y��ng)�� �c(di��n)����(bi��o).
�c(di��n)����(bi��o).�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
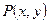 ��
�� �������c(di��n)
�������c(di��n) �ľ��x�c��
�ľ��x�c�� �S�ľ��x֮���
�S�ľ��x֮��� .
. ��܉�E
��܉�E �ķ��̣�
�ķ��̣� ��
�� ��
�� �σɄ�(d��ng)�c(di��n)����
�σɄ�(d��ng)�c(di��n)���� ,���C��ֱ��
,���C��ֱ�� ���^(gu��)һ��
���^(gu��)һ���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
 x, ��y=2����y=2x+1�����О顰B��ֱ�������� .�������������_�Y(ji��)Փ����̖(h��o)��
x, ��y=2����y=2x+1�����О顰B��ֱ�������� .�������������_�Y(ji��)Փ����̖(h��o)���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
 �ľ��x������ֱ��
�ľ��x������ֱ�� �ľ��xС2���t�c(di��n)P��܉�E������ .
�ľ��xС2���t�c(di��n)P��܉�E������ .�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
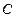 ��
��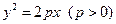 �cֱ��
�cֱ��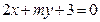 �ཻ��
�ཻ��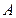 ��
��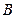 ���c(di��n)����?hu��)��タ
���c(di��n)����?hu��)��タ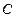 �Ľ��c(di��n)
�Ľ��c(di��n)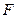 ��A�ġ�
��A�ġ�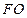 ��돽��
��돽��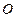 ������(bi��o)ԭ�c(di��n)������
������(bi��o)ԭ�c(di��n)������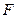 ����
����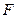 �քe�c����
�քe�c����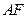 ��
��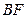 �ཻ��
�ཻ��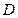 ��
��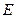 ���c(di��n)���t
���c(di��n)���t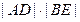 ��ֵ��
��ֵ�� �鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com