
(本小題滿分14分)
 如圖5,在直角梯形ABCP中,AP//BC,AP
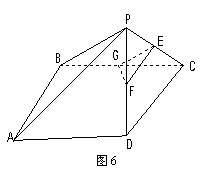
如圖5,在直角梯形ABCP中,AP//BC,AP![]() AB,AB=BC=
AB,AB=BC=![]() ,D是AP的中點,E,F(xiàn),G分別為PC、PD、CB的中點,將
,D是AP的中點,E,F(xiàn),G分別為PC、PD、CB的中點,將![]() 沿CD折起,使得
沿CD折起,使得![]() 平面ABCD, 如圖6.
平面ABCD, 如圖6.
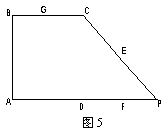 (Ⅰ)求證:AP//平面EFG;
(Ⅰ)求證:AP//平面EFG;
(Ⅱ) 求二面角![]() 的大小;
的大小;
(Ⅲ)求三棱椎![]() 的體積.
的體積.
(本小題滿分14分)
.解:(Ⅰ) 證明:方法一)連AC,BD交于O點,連GO,FO,EO.
∵E,F分別為PC,PD的中點,∴![]() //
//![]() ,同理
,同理![]() //
//![]() ,
, ![]() //
// ![]()
![]() 四邊形EFOG是平行四邊形,
四邊形EFOG是平行四邊形, ![]() 平面EFOG. ……3分
平面EFOG. ……3分
又在三角形PAC中,E,O分別為PC,AC的中點,![]() PA//EO……4分
PA//EO……4分
![]() 平面EFOG,PA
平面EFOG,PA![]() 平面EFOG, ……5分
平面EFOG, ……5分
![]() PA//平面EFOG,即PA//平面EFG. ……6分
PA//平面EFOG,即PA//平面EFG. ……6分
方法二) 連AC,BD交于O點,連GO,FO,EO.
∵E,F分別為PC,PD的中點,∴![]() //
//![]() ,同理
,同理![]() //
//![]()
 又
又![]() //AB,
//AB,![]() //
//![]()
![]() 平面EFG//平面PAB, ……4分
平面EFG//平面PAB, ……4分
又PA![]() 平面PAB,
平面PAB,![]() 平面EFG. ……6分
平面EFG. ……6分
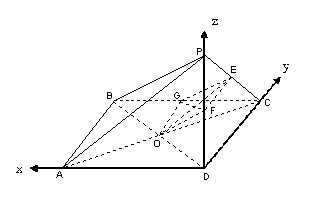
方法三)如圖以D為原點,以![]()
為方向向量建立空間直角坐標(biāo)系![]() .
.
則有關(guān)點及向量的坐標(biāo)為:
![]()
![]() ……2分
……2分
設(shè)平面EFG的法向量為![]()
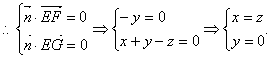 取
取![]() .……4分
.……4分
∵![]() ,……5分
,……5分
又![]() 平面EFG.
平面EFG.![]() AP//平面EFG. ……6分
AP//平面EFG. ……6分
(Ⅱ)由已知底面ABCD是正方形
![]()
![]() ,又∵
,又∵![]() 面ABCD
面ABCD ![]()
又![]()
![]() 平面PCD,
平面PCD,
![]() 向量
向量![]() 是平面PCD的一個法向量,
是平面PCD的一個法向量, ![]() =
=![]() ……8分
……8分
又由(Ⅰ)方法三)知平面EFG的法向量為![]() ……9分
……9分
 ……10分
……10分
結(jié)合圖知二面角![]() 的平面角為
的平面角為![]() ……11分
……11分
(Ⅲ)![]() ……14分
……14分


 寒假學(xué)與練系列答案
寒假學(xué)與練系列答案科目:高中數(shù)學(xué) 來源:2014屆江西省高二第一次月考理科數(shù)學(xué)試卷(解析版) 題型:解答題
(本小題滿分14分)
在醫(yī)學(xué)生物學(xué)試驗中,經(jīng)常以果蠅作為試驗對象.一個關(guān)有6只果蠅的籠子里,不慎混入了兩只蒼蠅(此時籠內(nèi)共有8只蠅子:6只果蠅和2只蒼蠅),只好把籠子打開一個小孔,讓蠅子一只一只地往外飛,直到兩只蒼蠅都飛出,再關(guān)閉小孔.
(Ⅰ)求籠內(nèi)恰好剩下1只果蠅的概率;
(Ⅱ)求籠內(nèi)至少剩下5只果蠅的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本小題滿分14分)
設(shè)函數(shù)![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)當(dāng)![]() 時,不等式恒成立,求實數(shù)
時,不等式恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)關(guān)于![]() 的方程
的方程![]() 在
在![]() 上恰有兩個相異實根,求
上恰有兩個相異實根,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本小題滿分14分)
已知![]() (m為常數(shù),m>0且
(m為常數(shù),m>0且![]() )
)
設(shè)![]() 是首項為4,公差為2的等差數(shù)列.
是首項為4,公差為2的等差數(shù)列.
(1)求證:數(shù)列{an}是等比數(shù)列;
(2)若bn=an·![]() ,且數(shù)列{bn}的前n項和Sn,當(dāng)
,且數(shù)列{bn}的前n項和Sn,當(dāng)![]() 時,求Sn;
時,求Sn;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本小題滿分14分)
已知定點![]() 和定直線
和定直線![]() ,
,![]() 是定直線
是定直線![]() 上的兩個動點且滿足
上的兩個動點且滿足![]() ,動點
,動點![]() 滿足
滿足![]() ,
,![]() (其中
(其中![]() 為坐標(biāo)原點).
為坐標(biāo)原點).
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 與
與![]() 相交于
相交于![]() 兩點
兩點
①求![]() 的值;
的值;
②設(shè)![]() ,當(dāng)三角形
,當(dāng)三角形![]() 的面積
的面積![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本小題滿分14分)
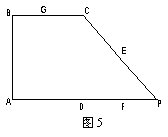
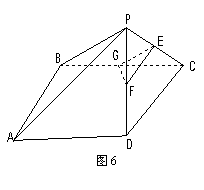 如圖5,在直角梯形ABCP中,AP//BC,AP
如圖5,在直角梯形ABCP中,AP//BC,AP![]() AB,AB=BC=
AB,AB=BC=![]() ,D是AP的中點,E,F(xiàn),G分別為PC、PD、CB的中點,將
,D是AP的中點,E,F(xiàn),G分別為PC、PD、CB的中點,將![]() 沿CD折起,使得
沿CD折起,使得![]() 平面ABCD, 如圖6.
平面ABCD, 如圖6.
 (Ⅰ)求證:AP//平面EFG;
(Ⅰ)求證:AP//平面EFG;
(Ⅱ) 求二面角![]() 的大小;
的大小;
(Ⅲ)求三棱椎![]() 的體積.
的體積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com