Question

在的二項展開式中，含x的奇次冪的項之和為S，當時，S=（ ）
A．2³⁰¹⁴
B．-2³⁰¹⁴
C．2³⁰¹⁵
D．-2³⁰¹⁵

Answer 1

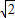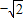【答案】分析：利用二項式定理將二項式展開，令x分別取 ，得到兩個等式，兩式相減，化簡即可求s的值．
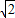解答：解：設（x-）²⁰⁰¹⁰=ax²⁰¹⁰+a₁x²⁰⁰⁹+…+a₂₀₀₉x+a₂₀₁₀
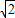則當x=時，有a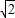（ ）²⁰¹⁰+a₁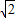（ ）²⁰⁰⁹+…+a₂₀₀₉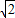（ ）+a₂₀₁₀=0      （1）
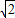當x=-時，有a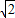（ ）²⁰¹⁰-a₁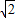（ ）²⁰⁰⁹+…-a₂₀₀₉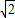（ ）+a₂₀₁₀=2³⁰¹⁵ （2）
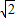（1）-（2）有a₁（ ）²⁰⁰⁹+…+a₂₀₀₉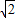（ ）=-2³⁰¹⁵¸
即2S=-2³⁰¹⁵則S=-2³⁰¹⁴
故選B．
點評：本題主要考查二項式定理的展開式形式及賦值法求系數和，同時考查了計算能力，屬于中檔題．