
 中,已知內角A、B、C所對的邊分別為a、b、c,且滿足2sinB(2cos2
中,已知內角A、B、C所對的邊分別為a、b、c,且滿足2sinB(2cos2 -1)=-
-1)=- cos2B.
cos2B. ,求
,求 的面積
的面積 的最大值.
的最大值.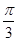 ;(2)△ABC的面積最大值為
;(2)△ABC的面積最大值為 。
。 -1)=-
-1)=- cos2B可得2sinBcosB=-
cos2B可得2sinBcosB=- cos2B,從而得tan2B=-
cos2B,從而得tan2B=- ,得2B=
,得2B=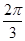 ,∴B=
,∴B=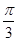 .
.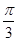 ,b=2,所以由余弦定理4=a2+c2-ac≥2ac-ac=ac,從而得出ac的最大值為4,故面積最大值確定.
,b=2,所以由余弦定理4=a2+c2-ac≥2ac-ac=ac,從而得出ac的最大值為4,故面積最大值確定. -1)=-
-1)=- cos2BÞ2sinBcosB=-
cos2BÞ2sinBcosB=- cos2B Þ tan2B=-
cos2B Þ tan2B=- ……4分
……4分 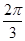 ,∴B=
,∴B=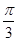 ……6分
……6分 Þ B=
Þ B=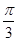
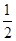 acsinB=
acsinB=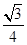 ac≤
ac≤
 ……14
……14

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com