
的切線(xiàn)在Y軸上的截距為bn,數(shù)列{an}滿(mǎn)足:a1=2,an+1=f-1(an)(n∈N*).
(1)求數(shù)列{an}的通項(xiàng)公式;
(2)在數(shù)列{![]() }中,僅當(dāng)n=5時(shí),
}中,僅當(dāng)n=5時(shí),![]() 取最小值,求A的取值范圍;
取最小值,求A的取值范圍;
(3)令函數(shù)g(x)=f-1(x)(1+x)2,數(shù)列{cn}滿(mǎn)足:c1=![]() ,cn+1=g(cn)(n∈N*),求證:對(duì)于一切
,cn+1=g(cn)(n∈N*),求證:對(duì)于一切
n≥2的正整數(shù),都滿(mǎn)足:1<![]() <2.
<2.
(文)已知函數(shù)f(x):![]() (0<x<1)的反函數(shù)為f-1(x),數(shù)列{an}滿(mǎn)足:a1=2,an+1=f-1(an) (n∈N*).
(0<x<1)的反函數(shù)為f-1(x),數(shù)列{an}滿(mǎn)足:a1=2,an+1=f-1(an) (n∈N*).
(1)求數(shù)列{an}的通項(xiàng)公式;
(2)設(shè)函數(shù)g(x)=f-1(x)(1+x)2在點(diǎn)(n,g(n))(n∈N*)處的切線(xiàn)在Y軸上的截距為bn,求數(shù)列{bn}的通項(xiàng)公式;
(3)在數(shù)列{bn+![]() }中,僅當(dāng)n=5時(shí),bn+
}中,僅當(dāng)n=5時(shí),bn+![]() 取最大值,求λ的取值范圍.
取最大值,求λ的取值范圍.
答案:(理)(1)∵f(x)=![]() ,
,
∴函數(shù)f(x)=![]() (0<x<1)的反函數(shù)為
(0<x<1)的反函數(shù)為
f-1(x)=![]() (x>0).
(x>0).
則an+1=f-1(an)=![]() ,
,
得![]() +1,即
+1,即![]() =1,
=1,
∴數(shù)列{![]() }是以2為首項(xiàng)、1為公差的等差數(shù)列,故an=
}是以2為首項(xiàng)、1為公差的等差數(shù)列,故an=![]() .
.
(2)又∵[f-1(x)]′=![]() .
.
∴函數(shù)f-1(x)在點(diǎn)(n,f-1(n))(n∈N*)處的切線(xiàn)方程為:y-f-1(n)=![]() (x-n),
(x-n),
令x=0,得bn=![]()
∴![]() =n2+λ(n+1)=(n+
=n2+λ(n+1)=(n+![]() )2+λ
)2+λ![]() ,
,
僅當(dāng)n=5時(shí)取最小值,只需4.5<![]() <5.5,解得-11<λ<-9.
<5.5,解得-11<λ<-9.
故A的取值范圍為(-11,-9).
(3)∵g(x)=f-1(x)(1+x)2=x(1+x),
故cn+1=g(cn)=cn(1+cn),
又∵c1=![]() >0,故cn>0,
>0,故cn>0,
則![]() ,
,
即![]() ,
,
∴![]()
=(![]() )+(
)+(![]() )+…+(
)+…+(![]() )
)
=![]() ,
,
又![]()
>![]()
=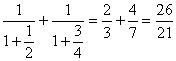 >1,
>1,
故1<![]() +…+
+…+![]() <2.
<2.
(文)(1)∵f(x)=![]() ,
,
∴函數(shù)f(x)=![]() (0<x<1)的反函數(shù)為f-1(x)=
(0<x<1)的反函數(shù)為f-1(x)=![]() (x>0).
(x>0).
貝an+1=f-1(an)=![]() ,得
,得![]() +1,即
+1,即![]() =1,
=1,
∴數(shù)列{![]() }是以2為首項(xiàng)、1為公差的等差數(shù)列,故an=
}是以2為首項(xiàng)、1為公差的等差數(shù)列,故an=![]() .
.
(2)∵g(x)=f-1(x)(1+x)2=![]() (1+x)2=x+x2,
(1+x)2=x+x2,
∴g′(x)=1+2x,即在點(diǎn)(n,g(n))處切線(xiàn)的斜率k=g′(n)=1+2n,
∴切線(xiàn)方程為y-g(n)=(1+2n)(x-n),
令x=0,得bn=g(n)-n-2n2=-n2.
(3)bn+![]() =-n2+λ(n+1)=-(n
=-n2+λ(n+1)=-(n![]() )2+λ+
)2+λ+![]() 僅在n=5時(shí)取最大值,只需4.5<
僅在n=5時(shí)取最大值,只需4.5<![]() <5.5,解得9<λ<11.
<5.5,解得9<λ<11.
故λ的取值范圍為(9,11).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:

 (理)已知函數(shù)f(x)=
(理)已知函數(shù)f(x)=| ln(2-x2) |
| |x+2|-2 |
| AB |
| AD |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
| sin2x-(a-4)(sinx-cosx)+a |
| π |
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 (2011•普陀區(qū)三模)(理)已知函數(shù)f(x)=
(2011•普陀區(qū)三模)(理)已知函數(shù)f(x)=| ln(2-x2) | |x+2|-2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
| ||
| 1-x |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| sinα | ||
|
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com