Question

如圖，四邊形 ABCD 為菱形，四邊形 CEFB 為正方形，平面 ABCD⊥平面CEFB,CE=1,∠AED=30°，則異面直線BC與AE所成角的大小_________

Answer 1

解析試題分析：先通過平移將兩條異面直線平移到同一個起點A，得到的銳角或直角就是異面直線所成的角，在三角形中再利用正弦定理求出此角即可．由題意，正方形和菱形變成均為1，又平面ABCD⊥平面CEFB，所以CE⊥平面ABCD，于是CE⊥CD，從而DE=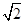
在△ADE中，AD=1，DE=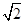，∠AED=30°，由正弦定理可知
故∠DAE=45°,又BC∥AD，故異面直線BC與AE所成角等于∠DAE,故答案為：45°
考點：異面直線所成角的求解
點評:直線a，b是異面直線，經(jīng)過空間一點O，分別引直線A∥a，B∥b，相交直線A，B所成的銳角（或直角）叫做異面直線a，b所成的角．求兩條異面直線所成角的大小一般方法是通過平行移動直線，把異面問題轉(zhuǎn)化為共面問題來解決