
(1)求證:AD∥平面A1BC;
(2)求證:平面A1MC⊥平面A1BD1;
(3)求點A到平面A1MC的距離.
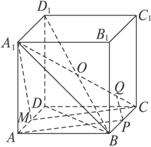
解法1:(1)證明如下:由已知AD∥BC,而BC在平面A1BC內(nèi),AD在平面A1BC外,所以AD∥平面A1BC.
(2)證明如下:連結(jié)BD,得△DAB∽△CDM,
∴∠ADB=∠DCM.由![]() =
=![]() ,∠DAB=∠CDM.
,∠DAB=∠CDM.
又∠DCM+∠DMC=90°,
∴∠ADB+∠DMC=90°.故BD⊥CM,又BD是BD1在平面ABCD上的射影,
由三垂線定理可知BD1⊥CM.
同理可得BD1⊥A1M,

∴BD1⊥平面A1MC.又BD1![]() 平面A1BD1,
平面A1BD1,
∴平面A1MC⊥平面A1BD1.
(3)取BC的中點P,設O為A1C與BD1的交點,OC的中點Q,連結(jié)AP、PQ,由AP∥MC知點A到平面A1MC的距離等于點P到平面A1MC的距離,由P、Q分別是BC、OC的中點知PQ∥BO,PQ=![]() BO.又BO⊥平面A1MC,∴PQ⊥平面A1MC.而BO=a,∴PQ=
BO.又BO⊥平面A1MC,∴PQ⊥平面A1MC.而BO=a,∴PQ=![]() a,即點A到平面A1MC的距離為
a,即點A到平面A1MC的距離為![]() a.
a.
解法2:以D為原點,以射線DA、DC、DD1分別為x、y、z軸的正半軸建立空間直角坐標系,可知各點坐標分別為D(0,0,0),A(![]() a,0,0),B(
a,0,0),B(![]() a,0,0),C(0,a,0),
a,0,0),C(0,a,0),
M(![]() a,0,0),D1(0,0,a),A1(
a,0,0),D1(0,0,a),A1(![]() a,0,a).
a,0,a).
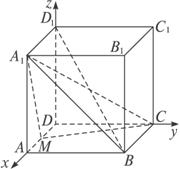
(1)由此可得![]() =(
=(![]() a,0,0),
a,0,0),![]() =(
=(![]() a,-a,0),
a,-a,0),
所以![]() =
=![]() .故
.故![]() ∥
∥![]() .而BC在平面A1BC內(nèi),AD在平面A1BC外,所以AD∥平面A1BC.
.而BC在平面A1BC內(nèi),AD在平面A1BC外,所以AD∥平面A1BC.
(2)![]() =(
=(![]() a,0,a),
a,0,a),![]() =(
=(![]() ,-a,0),
,-a,0), ![]() ·
·![]() =0,故BD1⊥CM.同理可得BD1⊥A1M,∴BD1⊥平面A1MC.又BD1
=0,故BD1⊥CM.同理可得BD1⊥A1M,∴BD1⊥平面A1MC.又BD1![]() 平面A1BD1,∴平面A1MC⊥平面A1BD1.
平面A1BD1,∴平面A1MC⊥平面A1BD1.
(3)![]() =(
=(![]() ,0,0),
,0,0),![]() =(
=(![]() a,0,-a)由(2)知
a,0,-a)由(2)知![]() 是平面A1MC的法向量.
是平面A1MC的法向量.
∴點A到平面A1MC的距離為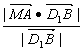
![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源: 題型:
 如圖,定義八個頂點都在某圓柱的底面圓周上的長方體叫做圓柱的內(nèi)接長方體,圓柱也叫長方體的外接圓柱.設長方體ABCD-A1B1C1D1的長、寬、高分別為a,b,c(其中a>b>c),那么該長方體的外接圓柱側(cè)面積的最大值等于( )
如圖,定義八個頂點都在某圓柱的底面圓周上的長方體叫做圓柱的內(nèi)接長方體,圓柱也叫長方體的外接圓柱.設長方體ABCD-A1B1C1D1的長、寬、高分別為a,b,c(其中a>b>c),那么該長方體的外接圓柱側(cè)面積的最大值等于( )查看答案和解析>>
科目:高中數(shù)學 來源: 題型:

A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:

A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:高中數(shù)學 來源:2010-2011年四川省成都市高二3月月考數(shù)學試卷 題型:填空題
(文科做)(本題滿分14分)如圖,在長方體
ABCD—A1B1C1D1中,AD=AA1=1,AB=2,點E在棱AB上移動.
(1)證明:D1E⊥A1D;
(2)當E為AB的中點時,求點E到面ACD1的距離;
(3)AE等于何值時,二面角D1—EC-D的大小為 .
.

(理科做)(本題滿分14分)
如圖,在直三棱柱ABC – A1B1C1中,∠ACB = 90°,CB = 1,
CA = ,AA1 =
,AA1 = ,M為側(cè)棱CC1上一點,AM⊥BA1.
,M為側(cè)棱CC1上一點,AM⊥BA1.
(Ⅰ)求證:AM⊥平面A1BC;
(Ⅱ)求二面角B – AM – C的大小;
(Ⅲ)求點C到平面ABM的距離.

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com