
若數列![]() 滿足:
滿足:![]() 是常數),則稱數列
是常數),則稱數列![]() 為二階線性遞推數列,且定義方程
為二階線性遞推數列,且定義方程![]() 為數列
為數列![]() 的特征方程,方程的根稱為特征根; 數列
的特征方程,方程的根稱為特征根; 數列![]() 的通項公式
的通項公式![]() 均可用特征根求得:
均可用特征根求得:
①若方程![]() 有兩相異實根
有兩相異實根![]() ,則數列通項可以寫成
,則數列通項可以寫成![]() ,(其中
,(其中![]() 是待定常數);
是待定常數);
②若方程![]() 有兩相同實根
有兩相同實根![]() ,則數列通項可以寫成
,則數列通項可以寫成![]() ,(其中
,(其中![]() 是待定常數);
是待定常數);
再利用![]() 可求得
可求得![]() ,進而求得
,進而求得![]() .
.
根據上述結論求下列問題:
(1)當![]() ,
,![]() (
(![]() )時,求數列
)時,求數列![]() 的通項公式;
的通項公式;
(2)當![]() ,
,![]() (
(![]() )時,求數列
)時,求數列![]() 的通項公式;
的通項公式;
(3)當![]() ,
,![]() (
(![]() )時,記
)時,記![]() ,若
,若![]() 能被數
能被數![]() 整除,求所有滿足條件的正整數
整除,求所有滿足條件的正整數![]() 的取值集合.
的取值集合.
(1) ![]() (2)
(2)![]()
(3)![]()
(1)由![]() 可知特征方程為:
可知特征方程為:
![]() ,
, ![]() …………………3分
…………………3分
所以 設 ![]() ,由
,由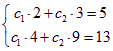 得到
得到![]() ,
,
所以 ![]() ; …………………6分
; …………………6分
(2)由![]() 可以得到
可以得到![]()
設![]() ,則上述等式可以化為:
,則上述等式可以化為:![]() …………………8分
…………………8分
![]() ,所以
,所以![]() 對應的特征方程為:
對應的特征方程為:
![]() ,
,![]() …………………10分
…………………10分
所以令 ![]() ,由
,由![]() 可以得出
可以得出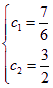
所以![]() …………………11分
…………………11分
即 ![]() …………………12分
…………………12分
(3)同樣可以得到通項公式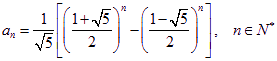 ………14分
………14分
所以![]()
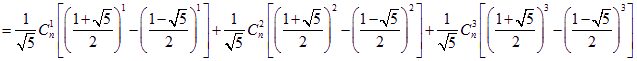

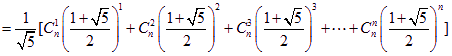
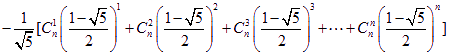
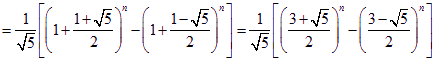
即 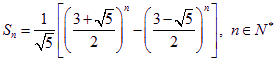 …………………14分
…………………14分
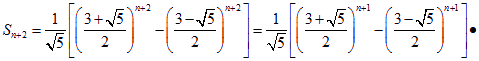
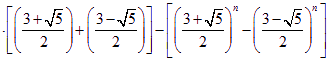
![]()
即 ![]() ,
,![]() …………………16分
…………………16分
因此![]() 除以
除以![]() 的余數,完全由
的余數,完全由![]() 除以
除以![]() 的余數確定,
的余數確定,
因為![]()
![]() 所以
所以 ![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
由以上計算及![]() 可知,數列
可知,數列![]() 各項除以
各項除以![]() 的余數依次是:
的余數依次是:
![]() 它是一個以
它是一個以![]() 為周期的數列,從而
為周期的數列,從而![]() 除以
除以![]() 的余數等價于
的余數等價于![]() 除以
除以![]() 的余數,所以
的余數,所以![]() ,
,![]() ,
,
即所求集合為:![]() …………………18分
…………………18分


 導學全程練創優訓練系列答案
導學全程練創優訓練系列答案科目:高中數學 來源: 題型:
數列![]() 滿足
滿足![]() ,
,![]() 是常數.
是常數.
⑴當![]() 時,求
時,求![]() 及
及![]() 的值;
的值;
⑵數列![]() 是否可能為等差數列?若可能,求出它的通項公式;若不可能,說明理由;
是否可能為等差數列?若可能,求出它的通項公式;若不可能,說明理由;
⑶求![]() 的取值范圍,使得存在正整數
的取值范圍,使得存在正整數![]() ,當
,當![]() 時總有
時總有![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分)
數列![]() 滿足
滿足![]() ,
,![]() 是常數.
是常數.
(1)數列![]() 是否可能為等差數列?若可能,求出它的通項公式;若不可能,說明理由;
是否可能為等差數列?若可能,求出它的通項公式;若不可能,說明理由;
(2)求![]() 的取值范圍,使得存在正整數
的取值范圍,使得存在正整數![]() ,當
,當![]() 時總有
時總有![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本題滿分18分,第(1)小題6分,第(2)小題6分,第(3)小題6分)
若數列![]() 滿足:
滿足:![]() 是常數),則稱數列
是常數),則稱數列![]() 為二階線性遞推數列,且定義方程
為二階線性遞推數列,且定義方程![]() 為數列
為數列![]() 的特征方程,方程的根稱為特征根; 數列
的特征方程,方程的根稱為特征根; 數列![]() 的通項公式
的通項公式![]() 均可用特征根求得:
均可用特征根求得:
①若方程![]() 有兩相異實根
有兩相異實根![]() ,則數列通項可以寫成
,則數列通項可以寫成![]() ,(其中
,(其中![]() 是待定常數);
是待定常數);
②若方程![]() 有兩相同實根
有兩相同實根![]() ,則數列通項可以寫成
,則數列通項可以寫成![]() ,(其中
,(其中![]() 是待定常數);
是待定常數);
再利用![]() 可求得
可求得![]() ,進而求得
,進而求得![]() .
.
根據上述結論求下列問題:
(1)當![]() ,
,![]() (
(![]() )時,求數列
)時,求數列![]() 的通項公式;
的通項公式;
(2)當![]() ,
,![]() (
(![]() )時,求數列
)時,求數列![]() 的通項公式;
的通項公式;
(3)當![]() ,
,![]() (
(![]() )時,記
)時,記![]() ,若
,若![]() 能被數
能被數![]() 整除,求所有滿足條件的正整數
整除,求所有滿足條件的正整數![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中數學 來源:河北省2010年高三一模模擬(三)數學理 題型:解答題
(本小題滿分12分)
數列 滿足
滿足 ,
, 是常數.
是常數.
(1)數列 是否可能為等差數列?若可能,求出它的通項公式;若不可能,說明理由;
是否可能為等差數列?若可能,求出它的通項公式;若不可能,說明理由;
(2)求 的取值范圍,使得存在正整數
的取值范圍,使得存在正整數 ,當
,當 時總有
時總有 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com