
已知函數f(x)=sin2 +
+ sin
sin
 -
- .
.
(1)在△ABC中,若sin C=2sin A,B為銳角且有f(B)= ,求角A,B,C;
,求角A,B,C;
(2)若f(x)(x>0)的圖象與直線y= 交點的橫坐標由小到大依次是x1,x2,…,xn,求數列{xn}的前2n項和,n∈N*.
交點的橫坐標由小到大依次是x1,x2,…,xn,求數列{xn}的前2n項和,n∈N*.
 新思維假期作業暑假吉林大學出版社系列答案
新思維假期作業暑假吉林大學出版社系列答案 藍天教育暑假優化學習系列答案
藍天教育暑假優化學習系列答案科目:高中數學 來源: 題型:解答題
設函數f(x)= -
- sin2ωx-sinωxcosωx(ω>0),且y=f(x)圖象的一個對稱中心到最近的對稱軸的距離為
sin2ωx-sinωxcosωx(ω>0),且y=f(x)圖象的一個對稱中心到最近的對稱軸的距離為 .
.
(1)求ω的值;
(2)求f(x)在區間[π, ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
函數f(x)=Asin  +1(A>0,ω>0)的最大值為3,其圖象相鄰兩條對稱軸之間的距離為
+1(A>0,ω>0)的最大值為3,其圖象相鄰兩條對稱軸之間的距離為 .
.
(1)求函數f(x)的解析式;
(2)設α∈ ,f
,f =2,求α的值.
=2,求α的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數f(x)=sin +sin
+sin +
+ cos ωx(其中ω>0),且函數f(x)的圖象的兩條相鄰的對稱軸間的距離為
cos ωx(其中ω>0),且函數f(x)的圖象的兩條相鄰的對稱軸間的距離為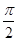 .
.
(1)求ω的值;
(2)將函數y=f(x)的圖象上各點的橫坐標伸長到原來的2倍,縱坐標不變,得到函數y=g(x)的圖象,求函數g(x)在區間 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數f(x)=msinx+cosx(x∈R)的圖象經過點( ,1).
,1).
(1)求f(x)的解析式,并求函數的最小正周期.
(2)若f(α+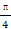 )=
)= 且α∈(0,
且α∈(0, ),求f(2α-
),求f(2α-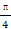 )的值.
)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)= sin ωx-sin2
sin ωx-sin2 +
+ (ω>0)的最小正周期為π.
(ω>0)的最小正周期為π.
(1)求ω的值及函數f(x)的單調遞增區間;
(2)當x∈ 時,求函數f(x)的取值范圍.
時,求函數f(x)的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com