
(本題滿分14分,第1小題6分,第2小題8分)
已知函數(shù)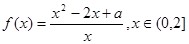 ,其中常數(shù)a > 0.
,其中常數(shù)a > 0.
(1) 當a = 4時,證明函數(shù)f(x)在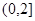 上是減函數(shù);
上是減函數(shù);
(2) 求函數(shù)f(x)的最小值.
(1)任取0<x1<x2≤2,則f(x1)–f(x2)=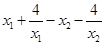
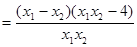 ,
,
因為0<x1<x2≤2,所以f(x1)–f(x2)>0,即f(x1)>f(x2);
(2)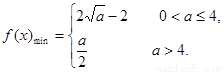 。
。
【解析】
試題分析:(1) 當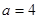 時,
時,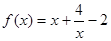 ,…………………………………………1分
,…………………………………………1分
任取0<x1<x2≤2,則f(x1)–f(x2)=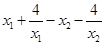
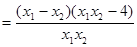 ………………3分
………………3分
因為0<x1<x2≤2,所以f(x1)–f(x2)>0,即f(x1)>f(x2)………………………………………5分
所以函數(shù)f(x)在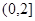 上是減函數(shù);………………………………………………………6分
上是減函數(shù);………………………………………………………6分
(2)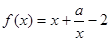
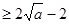 ,……………………………………………………7分
,……………………………………………………7分
當且僅當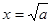 時等號成立,…………………………………………………………8分
時等號成立,…………………………………………………………8分
當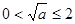 ,即
,即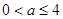 時,
時,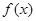 的最小值為
的最小值為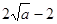 ,………………………10分
,………………………10分
當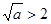 ,即
,即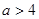 時,
時,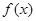 在
在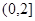 上單調遞減,…………………………………11分
上單調遞減,…………………………………11分
所以當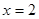 時,
時,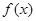 取得最小值為
取得最小值為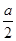 ,………………………………………………13分
,………………………………………………13分
綜上所述: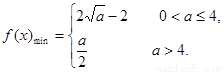 ………………………………………14分
………………………………………14分
考點:函數(shù)的單調性和最值;基本不等式。
點評:用定義法證明函數(shù)單調性的步驟:一設二作差三變形四判斷符號五得出結論,其中最重要的是四變形,最好變成幾個因式乘積的形式,這樣便于判斷符號。


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數(shù)學 來源: 題型:
(本題滿分14分,第(1)小題6分,第(2)小題8分)
四棱錐P-ABCD中,PD⊥平面ABCD,PA與平面ABCD所成的角為60![]() ,在四邊形ABCD中,∠ADC=∠DAB=90
,在四邊形ABCD中,∠ADC=∠DAB=90![]() ,AB=4,CD=1,AD=2.
,AB=4,CD=1,AD=2.

(1)求四棱錐P-ABCD的體積;
(2)求異面直線PA與BC所成的角.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
(本題滿分14分,第(1)小題4分,第(2)小題4分,第(2)小題6分)
設數(shù)列![]() 中,若
中,若![]() ,則稱數(shù)列
,則稱數(shù)列![]() 為“凸數(shù)列”。
為“凸數(shù)列”。
(1)設數(shù)列![]() 為“凸數(shù)列”,若
為“凸數(shù)列”,若![]() ,試寫出該數(shù)列的前6項,并求出該6項之和;
,試寫出該數(shù)列的前6項,并求出該6項之和;
(2)在“凸數(shù)列”![]() 中,求證:
中,求證:![]() ;
;
(3)設![]() ,若數(shù)列
,若數(shù)列![]() 為“凸數(shù)列”,求數(shù)列前
為“凸數(shù)列”,求數(shù)列前![]() 項和
項和![]() 。
。
查看答案和解析>>
科目:高中數(shù)學 來源:2012-2013學年上海市金山區(qū)高三上學期期末考試數(shù)學試卷(解析版) 題型:解答題
(本題滿分14分,第1小題6分,第2小題8分)
已知函數(shù) ,x∈R,且f(x)的最大值為1.
,x∈R,且f(x)的最大值為1.
(1) 求m的值,并求f(x)的單調遞增區(qū)間;
(2) 在△ABC中,角A、B、C的對邊a、b、c,若 ,且
,且 ,試判斷△ABC的形狀.
,試判斷△ABC的形狀.
查看答案和解析>>
科目:高中數(shù)學 來源:2010-2011學年上海市高三上學期期中考試數(shù)學卷 題型:解答題
(本題滿分14分,第1小題5分,第2小題9分)
一校辦服裝廠花費2萬元購買某品牌運動裝的生產與銷售權,根據(jù)以往經(jīng)驗,每生產1百套這種品牌運動裝的成本為1萬元,每生產x(百套)的銷售額R(x)(萬元)滿足:

(1)該服裝廠生產750套此種品牌運動裝可獲得利潤多少萬元?
(2)該服裝廠生產多少套此種品牌運動裝利潤最大?此時,利潤是多少萬元?
查看答案和解析>>
科目:高中數(shù)學 來源:上海市長寧區(qū)2010屆高三第二次模擬考試數(shù)學文 題型:解答題
(本題滿分14分,第(1)小題6分,第(2)小題8分)
設函數(shù) ,若不等式
,若不等式 的解集為
的解集為 。
。
(1)求 的值;
的值;
(2)若函數(shù) 在
在 上的最小值為1,求實數(shù)
上的最小值為1,求實數(shù) 的值。
的值。
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com