
(本題滿分14分) 本題共有2個小題,第1小題滿分6分,第2小題滿分8分.
(理)某種型號汽車四個輪胎半徑相同,均為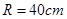 ,同側(cè)前后兩輪胎之間的距離(指輪胎中心之間距離)為
,同側(cè)前后兩輪胎之間的距離(指輪胎中心之間距離)為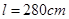 (假定四個輪胎中心構(gòu)成一個矩形). 當(dāng)該型號汽車開上一段上坡路
(假定四個輪胎中心構(gòu)成一個矩形). 當(dāng)該型號汽車開上一段上坡路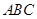 (如圖(1)所示,其中
(如圖(1)所示,其中 (
( )),且前輪
)),且前輪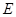 已在
已在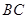 段上時,后輪中心在
段上時,后輪中心在 位置;若前輪中心到達(dá)
位置;若前輪中心到達(dá)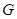 處時,后輪中心在
處時,后輪中心在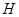 處(假定該汽車能順利駛上該上坡路). 設(shè)前輪中心在
處(假定該汽車能順利駛上該上坡路). 設(shè)前輪中心在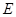 和
和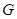 處時與地面的接觸點(diǎn)分別為
處時與地面的接觸點(diǎn)分別為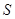 和
和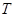 ,且
,且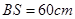 ,
,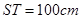 . (其它因素忽略不計(jì))
. (其它因素忽略不計(jì))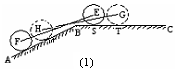
(1)如圖(2)所示,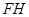 和
和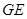 的延長線交于點(diǎn)
的延長線交于點(diǎn)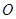 ,
,
求證: (cm);
(cm);
(2)當(dāng)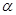 =
=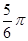 時,后輪中心從
時,后輪中心從 處移動到
處移動到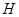 處實(shí)際移動了多少厘米? (精確到1cm)
處實(shí)際移動了多少厘米? (精確到1cm)
(1)由OE//BC,OH//AB,得∠EOH=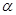 ,
, 
過點(diǎn)B作BM⊥OE,BN⊥OH,則Rt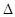 OMB
OMB Rt
Rt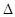 ONB,從而∠BOM=
ONB,從而∠BOM= .
.
在Rt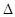 OMB中,由BM=40得OM=40cot
OMB中,由BM=40得OM=40cot ,從而,OE=OM+ME=OM+BS=
,從而,OE=OM+ME=OM+BS= .
.
(2)98cm。
解析試題分析:(1) 由OE//BC,OH//AB,得∠EOH=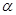 , 2分
, 2分
過點(diǎn)B作BM⊥OE,BN⊥OH,則
Rt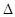 OMB
OMB Rt
Rt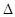 ONB,從而
ONB,從而
∠BOM= . 4分
. 4分
在Rt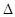 OMB中,由BM=40得OM=40cot
OMB中,由BM=40得OM=40cot ,從而,OE=OM+ME=OM+BS=
,從而,OE=OM+ME=OM+BS= . 6分
. 6分
(2)由(1)結(jié)論得OE= .
.
設(shè)OH=x,OF=y,
在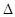 OHG中,由余弦定理得,
OHG中,由余弦定理得,
2802=x2+( +100)2-2x(
+100)2-2x( +100)cos1500 ,
+100)cos1500 ,
解得x 118.8cm. 9分
118.8cm. 9分
在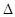 OEF中,由余弦定理得,
OEF中,由余弦定理得,
2802=y2+( )2-2y(
)2-2y( )cos1500 ,
)cos1500 ,
解得y 216.5cm. 12分
216.5cm. 12分
所以,F(xiàn)H=y-x 98cm,
98cm,
即后輪中心從F處移動到H處實(shí)際移動了約98cm. 14分
考點(diǎn):正弦定理;余弦定理;解三角形的實(shí)際應(yīng)用。
點(diǎn)評:在解應(yīng)用題時,我們要分析題意,分清已知與所求,再根據(jù)題意正確畫出示意圖,通過這一步可將實(shí)際問題轉(zhuǎn)化為可用數(shù)學(xué)方法解決的問題。解題中,要注意正、余弦定理的靈活應(yīng)用。



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分14分)
在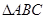 中,內(nèi)角A、B、C的對邊分別是
中,內(nèi)角A、B、C的對邊分別是 、b、c,已知
、b、c,已知 ,且
,且 的夾角為
的夾角為 。
。
(Ⅰ)求內(nèi)角C的大小;
(Ⅱ)已知 ,三角形的面積
,三角形的面積 ,求
,求 的值。
的值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)設(shè)銳角△ABC的三內(nèi)角A,B,C的對邊分別為 A,b,c,已知向量 ,
,
 ,且
,且 ∥
∥ .
.
(1) 求角A的大小;
(2) 若 ,
, ,且△ABC的面積小于
,且△ABC的面積小于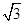 ,求角B的取值范圍.
,求角B的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)函數(shù)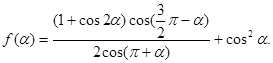
(1)設(shè)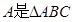 的內(nèi)角,且為鈍角,求
的內(nèi)角,且為鈍角,求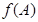 的最小值;
的最小值;
(2)設(shè) 是銳角
是銳角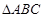 的內(nèi)角,且
的內(nèi)角,且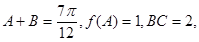 求
求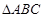 的三個內(nèi)角的大小和AC邊的長。
的三個內(nèi)角的大小和AC邊的長。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)
已知函數(shù)f(x)=" cos(" 2x+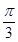 )+sin2x.
)+sin2x.
(Ⅰ)求函數(shù)f(x)的最小正周期和值域;
(Ⅱ)在△ABC中,角A、B、C的對邊分別為a、b、c,滿足
2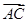 ·
·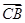 =
=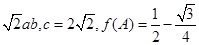 , 求△ABC的面積S.
, 求△ABC的面積S.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com