中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情
設拋物線y2＝2px(p＞ 0)的焦點為F，經過點F的直線交拋物線于A、B兩點.點C在拋物線的準線上，且BC∥x軸.證明直線 AC經過原點O.

思路解析：本題的解法很多，采用坐標方法進行代數推理，可以證明OA與OC的斜率相等，證明AO+OC=AC，證明OC與BF的交點A在拋物線上，證明AC的方程形如y=φ(p)x，等等，每種證明又有不同的表述形式，甚至可以用參數方程法，采用平面幾何方法進行推理.

證法一：如圖所示，

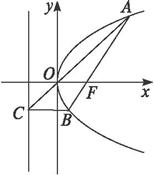
因為拋物線y2=2px(p＞0)的焦點為F（，0），所以經過點F的直線AB的方程可設為x=my+，代入拋物線方程得y2-2pmy-p2=0.

若記A(x1,y1)，B(x2,y2)，則y1,y2是該方程的兩個根，所以y1y2=-p2.

因為BC∥x軸，且點C在準線x=-上，所以點C的坐標為（-，y2）.

故直線CO的斜率為

k===,

即k也是直線OA的斜率，所以直線AC經過原點O.

證法二：設A(x1,y1)，B(x2,y2).

因為BC∥x軸，所以C（-，y2）.

因為A、B在拋物線上，

所以y12=2px1,y22=2px2.

又因為直線AB過焦點F，

所以kAF=kBF，即=.

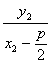所以.

所以y1y2(y2-y1)=p2(y1-y2).

因為y1≠y2，所以y1y2=-p2.

因為kOC=====kOA,

所以直線AC經過原點O.

證法三：因為拋物線y2=2px(p＞0)的焦點為（,0），

所以設直線AB的方程為x=ky+.

由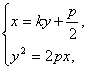

消去x得y2-2pky-p2=0.

所以yA·yB=-p2.

因為A（,yA）,C(-,yB),即C(-,-)，

所以直線AC的方程為=.

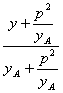化簡得y=x.

顯然，原點O適合此方程，所以原點O在直線AC上.

證法四：設B（a，b），則C(-,b)，F(,0),

所以直線BF的方程為y(a-)=b(x-)，

直線OC的方程為y=-x.

所以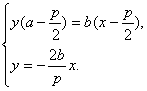

消y得-x(a-)=b(x-).

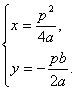所以所以A′(，-).

因為B在拋物線y2=2px上，所以b2=2ap.

所以A′(，-).

所以(-)2==2p·.

所以A′在拋物線y2=2px上.所以A′與A重合，即直線AC經過原點O.

證法五：如下圖所示，記x軸與拋物線準線l的交點為E，過A作AD⊥l，D是垂足，則AD∥FE∥BC.

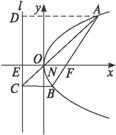
連結AC，與EF相交于點N，則，.

根據拋物線的性質,得|AF|=|AD|，|BF|=|BC|.

所以|EN|===|NF|,

即點N是EF的中點，與拋物線的頂點O重合，所以直線AC經過原點O.

證法六：如下圖所示，

設準線交x軸于點E，過A點作AM⊥x軸于M.

設A(x1,y1)，B(x2,y2)，則C（-,y2）,所以=.

由證法二知y1=，

又，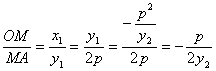

所以=.所以△AOM∽△COE.所以∠AOM=∠COE.

故A、O、C三點共線，即直線AC過原點O.


練習冊系列答案
相關習題

科目：高中數學 來源：設計選修數學－1-1蘇教版 蘇教版 題型：047

設拋物線y2＝2px(p＞0)的焦點為F，直線l過點F交拋物線于A、B兩點，點M在拋物線的準線上，O為坐標原點，設A(x1，y1)，B(x2，y2)．

(1)求證：y1y2＝－p2；

(2)求證：直線MA、MF、MB的斜率成等差數列．

查看答案和解析>>

科目：高中數學 來源：全優設計選修數學－2-2蘇教版 蘇教版 題型：047

設拋物線y2＝2px(p＞0)的焦點為F，經過點F的直線交拋物線于A，B兩點，點C在拋物線的準線上，且BC∥x軸，證明直線AC經過原點O．

查看答案和解析>>

科目：高中數學 來源：浙江省杭州學軍中學2009屆高三第十次月考數學(文)試題 題型：044

設拋物線y2＝2px(p＞0)的焦點為F，經過點F的直線交拋物線于A(x1，y1)、B(x2，y2)(y1＞0，y2＜0)兩點，M是拋物線的準線上的一點，O是坐標原點，若直線MA、MF、MB的斜率分別記為：kMA＝a、kMF＝b、kMB＝c，(如圖)

(1)若y1y2＝－4，求拋物線的方程；

(2)當b＝2時，求證：a＋c為定值．

查看答案和解析>>

科目：高中數學 來源：2010-2011學年云南省高二下學期期末考試理科數學卷 題型：填空題

設拋物線y2＝2Px（P＞0）的焦點為F，點A(0，2).若線段FA的中點B在拋物線上，則B到該拋物線準線的距離為        .

 

查看答案和解析>>

同步練習冊答案