
在平面直角坐標系中,對于任意相鄰三點都不共線的有序整點列(整點即橫縱坐標都是整數的點)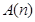 :
: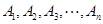 與
與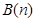 :
: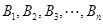 ,其中
,其中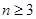 ,若同時滿足:①兩點列的起點和終點分別相同;②線段
,若同時滿足:①兩點列的起點和終點分別相同;②線段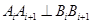 ,其中
,其中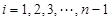 ,則稱
,則稱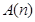 與
與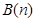 互為正交點列.
互為正交點列.
(1)求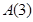 :
: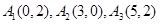 的正交點列
的正交點列 ;
;
(2)判斷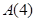 :
: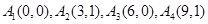 是否存在正交點列
是否存在正交點列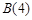 ?并說明理由;
?并說明理由;
(3)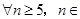 N,是否都存在無正交點列的有序整點列
N,是否都存在無正交點列的有序整點列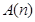 ?并證明你的結論.
?并證明你的結論.
(1)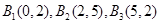 ,(2)不存在,(3)存在.
,(2)不存在,(3)存在.
解析試題分析:(1)因為 與
與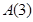 的起點和終點分別相同,所以
的起點和終點分別相同,所以 ,只需求
,只需求 .由
.由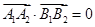 及
及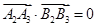 ,可解得
,可解得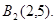 本題實質考查對新定義的理解.關鍵逐條代入驗證.(2)與(1)相似,從求
本題實質考查對新定義的理解.關鍵逐條代入驗證.(2)與(1)相似,從求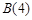 角度出發,能求出來就存在,否則就不存在.首先有
角度出發,能求出來就存在,否則就不存在.首先有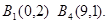 求
求 時,不是設四個未知數,二是利用向量垂直關系,設三個未知數,即
時,不是設四個未知數,二是利用向量垂直關系,設三個未知數,即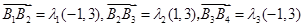 ,因為
,因為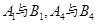 相同,所以有
相同,所以有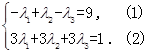 因為
因為
 ,所以方程組顯然不成立,即不存在.
,所以方程組顯然不成立,即不存在.
(3)按照(1)的思路,要保證方程組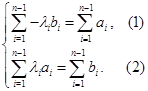 無解,須使得整數盡量取
無解,須使得整數盡量取 ,①當
,①當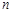 為偶數時,取
為偶數時,取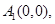
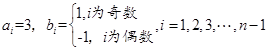 .②當
.②當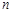 為奇數時,取
為奇數時,取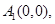
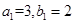 ,
,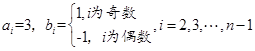 ,就可滿足題意.
,就可滿足題意.
試題解析:解:
(1)設點列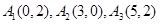 的正交點列是
的正交點列是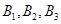 ,
,
由正交點列的定義可知 ,設
,設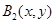 ,
,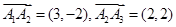 ,
,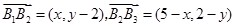 ,
,
由正交點列的定義可知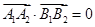 ,
,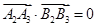 ,
,
即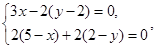 解得
解得
所以點列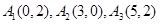 的正交點列是
的正交點列是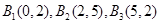 . 3分
. 3分
(2)由題可得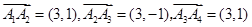 ,
,
設點列 是點列
是點列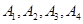 的正交點列,
的正交點列,
則可設 ,
,

因為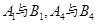 相同,所以有
相同,所以有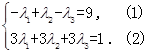
因為
 ,方程(2)顯然不成立,
,方程(2)顯然不成立,
所以有序整點列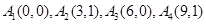 不存在正交點列; 8分
不存在正交點列; 8分
(3)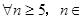
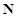 ,都存在整點列
,都存在整點列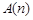 無正交點列. 9分
無正交點列. 9分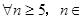
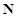 ,設
,設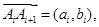 其中
其中 是一對互質整數,
是一對互質整數,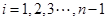
若有序整點列 是點列
是點列 正交點列,
正交點列,
則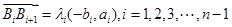 ,
,
則有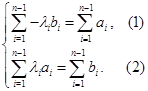
①當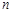 為偶數時,取
為偶數時,取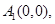
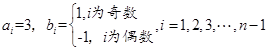 .
.
由于 是整點列,所以有
是整點列,所以有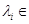
 ,
, .
.
等式(2)中左邊是3的倍數,右邊等于1,等式不成立,
所以該點列 無正交點列;
無正交點列;
②當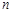 為奇數時,
為奇數時,
取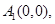


 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com