
(本小題滿分12分)
直線L1: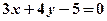 與直線L2:
與直線L2: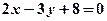 的交點(diǎn)為
的交點(diǎn)為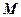
(1) 求經(jīng)過點(diǎn)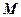 和原點(diǎn)的直線方程;
和原點(diǎn)的直線方程;
(2)求經(jīng)過點(diǎn)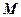 與直線
與直線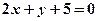 垂直的直線方程。
垂直的直線方程。
 數(shù)學(xué)奧賽暑假天天練南京大學(xué)出版社系列答案
數(shù)學(xué)奧賽暑假天天練南京大學(xué)出版社系列答案 南大教輔搶先起跑暑假銜接教程南京大學(xué)出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學(xué)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)已知直線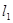 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)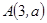 ,
,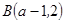 ,直線
,直線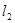 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)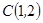 ,
,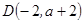 。
。
(1)若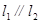 ,求
,求 的值。
的值。
(2)若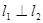 ,求
,求 的值。
的值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(1)證明:l經(jīng)過定點(diǎn);
(2)若直線l交x軸負(fù)半軸于A,交y軸正半軸于B,△AOB的面積為S,求S的最小值并求此時(shí)直線l的方程;
(3)若直線不經(jīng)過第三象限,求k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(滿分12分)
設(shè)直線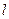 的方程為
的方程為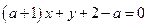
 。
。
(1)若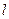 在兩坐標(biāo)軸上的截距相等
在兩坐標(biāo)軸上的截距相等 ,求
,求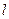 的方程;
的方程;
(2)若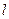 不經(jīng)過第二象限,求
不經(jīng)過第二象限,求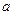 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題14分)已知P(2,1),直線l:x-y+4=0.
(1)求過點(diǎn)P與直線l平行的直線方程;
(2)求過點(diǎn)P與直線l垂直的直線方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
 已知兩點(diǎn)M、N分別在直線
已知兩點(diǎn)M、N分別在直線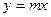 與直線
與直線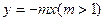 上運(yùn)動(dòng),且|MN|=2.動(dòng)點(diǎn)P滿足
上運(yùn)動(dòng),且|MN|=2.動(dòng)點(diǎn)P滿足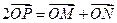 (O為坐標(biāo)原點(diǎn)),點(diǎn)P的軌跡記為曲線C.
(O為坐標(biāo)原點(diǎn)),點(diǎn)P的軌跡記為曲線C.
(I)求曲線C的方程;
(II)過點(diǎn)(0,1)作直線l與曲線C交于不同的兩點(diǎn)A、B.若對(duì)任意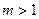 ,都有∠AOB為銳角,求直線l的斜率k的取值范圍.
,都有∠AOB為銳角,求直線l的斜率k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分14分)
已知點(diǎn) 及圓
及圓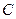 :
: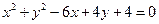 .
.
(Ⅰ)若直線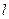 過點(diǎn)
過點(diǎn)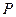 且與圓心
且與圓心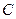 的距離為1,求直線
的距離為1,求直線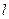 的方程;
的方程;
(Ⅱ)設(shè)過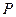 直線
直線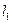 與圓
與圓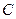 交于
交于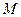 、
、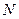 兩點(diǎn),當(dāng)
兩點(diǎn),當(dāng)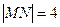 時(shí),求以
時(shí),求以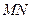 為直徑的圓的方程;
為直徑的圓的方程;
(Ⅲ)設(shè)直線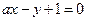 與圓
與圓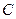 交于
交于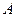 ,
,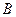 兩點(diǎn),是否存在實(shí)數(shù)
兩點(diǎn),是否存在實(shí)數(shù)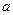 ,使得過點(diǎn)
,使得過點(diǎn) 的直線
的直線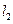 垂直平分
垂直平分 弦
弦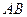 ?若存在,求出實(shí)數(shù)
?若存在,求出實(shí)數(shù)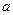 的值;若不存在,請(qǐng)說明理由.
的值;若不存在,請(qǐng)說明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com