
 平面CDE,AE=3.
平面CDE,AE=3.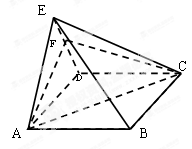
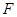 為
為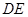 的中點,求證:
的中點,求證: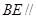 平面
平面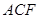 ;
;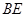 與平面
與平面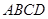 所成角的正弦值.
所成角的正弦值. 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案 單元加期末復習先鋒大考卷系列答案
單元加期末復習先鋒大考卷系列答案科目:高中數學 來源:不詳 題型:解答題
 ,且AB=2AD=2DC=2PD=4,E為PA的中點.
,且AB=2AD=2DC=2PD=4,E為PA的中點.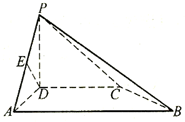
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 中,
中,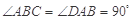 ,
,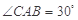 ,
,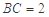 ,
,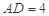 . 把
. 把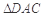 沿對角線
沿對角線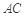 折起到
折起到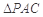 的位置,如圖2所示,使得點
的位置,如圖2所示,使得點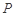 在平面
在平面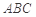 上的正投影
上的正投影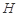 恰好落在線段
恰好落在線段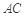 上,連接
上,連接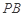 ,點
,點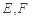 分別為線段
分別為線段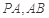 的中點.
的中點. 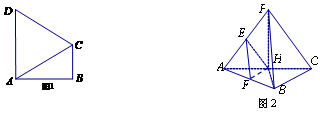
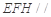 平面
平面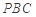 ;
;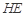 與平面
與平面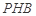 所成角的正弦值;
所成角的正弦值;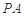 上是否存在一點
上是否存在一點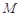 ,使得
,使得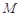 到點
到點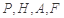 四點的距離相等?請說明理由.
四點的距離相等?請說明理由.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
A.如果平面 ,那么平面 ,那么平面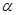 內一定存在直線平行于平面 內一定存在直線平行于平面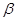 ; ; |
B.如果平面α不垂直于平面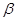 ,那么平面 ,那么平面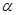 內一定不存在直線垂直于平面 內一定不存在直線垂直于平面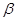 ; ; |
C.如果平面 ,平面 ,平面 , ,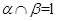 ,那么 ,那么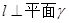 ; ; |
D.如果平面 ,那么平面 ,那么平面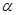 內所有直線都垂直于平面 內所有直線都垂直于平面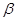 . . |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
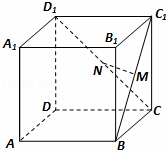
| A.MN與CC1垂直 | B.MN與AC垂直 | C.MN與BD平行 | D.MN與A1B1平行 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com