已知等比數列{an}各項都是正數,a1=3,a1+a2+a3=21,Sn為{an}的前n項和,
(Ⅰ)求通項an及Sn;
(Ⅱ)設{bn-an}是首項為1,公差為3的等差數列,求數列{bn}的通項公式及其前n項和Tn.
【答案】
分析:(Ⅰ)設等比數列{a
n}的公比為q,代入已知可得關于q的方程,解之可得q,代入等比數列的通項公式和求和公式可得;(Ⅱ)可得b
n=3×2
n-1+3n-2,分別由等差數列和等比數列的求和公式可得.
解答:解:(Ⅰ)設等比數列{a
n}的公比為q,則q>0,
代入已知可得3+3q+3q
2=21,解得q=2,或q=-3(舍去),
故a
n=3×2
n-1,S
n=
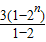
=3×2
n-1-3;
(Ⅱ)∵{b
n-a
n}是首項為1,公差為3的等差數列,
∴b
n-a
n=1+3(n-1)=3n-2,即b
n=3×2
n-1+3n-2
故T
n=3(1+2+2
2+…+2
n-1)+(1+4+7+…+3n-2)
=
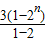
+
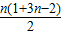
=3×2
n-3+
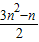 點評:
點評:本題考查等比數列和等差數列的求和公式,屬中檔題.

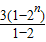 =3×2n-1-3;
=3×2n-1-3;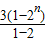 +
+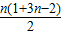 =3×2n-3+
=3×2n-3+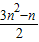


 閱讀快車系列答案
閱讀快車系列答案