
如圖所示,已知三棱錐A-BPC中,AP⊥PC,AC⊥BC,M為AB的中點(diǎn),D為PB的中點(diǎn),且△PMB為正三角形.
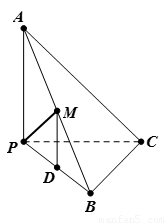
(1)求證:DM∥平面APC; (2)求證:平面ABC⊥平面APC.
(1)詳見解析;(2)詳見解析.
【解析】
試題分析:(1)要證明直線和平面平行,只需在平面內(nèi)找一條 直線與之平行,由已知得 是
是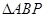 的中位線,所以
的中位線,所以 ,進(jìn)而證明
,進(jìn)而證明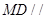 平面
平面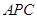 ;(2)要證明面面垂直,只需在一個平面內(nèi)找到另一個平面的一條垂線即可,由等邊三角形
;(2)要證明面面垂直,只需在一個平面內(nèi)找到另一個平面的一條垂線即可,由等邊三角形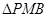 及
及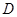 為
為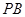 的中點(diǎn),則
的中點(diǎn),則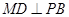 ,進(jìn)而說明
,進(jìn)而說明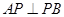 ,進(jìn)而說明
,進(jìn)而說明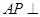 平面
平面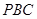 ,則有
,則有 ,又由已知
,又由已知 可證
可證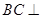 平面
平面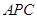 ,進(jìn)而證明結(jié)論.
,進(jìn)而證明結(jié)論.
試題解析:(1)由已知,得 是
是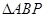 的中位線,所以
的中位線,所以 ,又
,又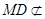 平面
平面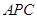 ,
,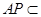 平面
平面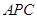 ,故
,故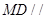 平面
平面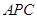 .
.
(2)因?yàn)?img src="http://thumb.zyjl.cn//pic6/res/gzsx/web/STSource/2014031104404071834235/SYS201403110441133746282707_DA.files/image006.png">為正三角形,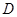 為
為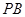 的中點(diǎn),所以
的中點(diǎn),所以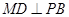 .所以
.所以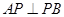 .又
.又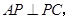
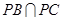
所以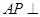 平面
平面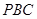 .因?yàn)?img src="http://thumb.zyjl.cn//pic6/res/gzsx/web/STSource/2014031104404071834235/SYS201403110441133746282707_DA.files/image020.png">平面
.因?yàn)?img src="http://thumb.zyjl.cn//pic6/res/gzsx/web/STSource/2014031104404071834235/SYS201403110441133746282707_DA.files/image020.png">平面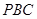 ,所以
,所以 .又
.又
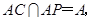 所以
所以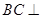 平面
平面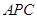 .因?yàn)?img src="http://thumb.zyjl.cn//pic6/res/gzsx/web/STSource/2014031104404071834235/SYS201403110441133746282707_DA.files/image020.png">平面
.因?yàn)?img src="http://thumb.zyjl.cn//pic6/res/gzsx/web/STSource/2014031104404071834235/SYS201403110441133746282707_DA.files/image020.png">平面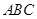 ,所以平面
,所以平面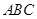 ⊥平面
⊥平面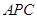 .
.
考點(diǎn):1、直線和平面平行的判定;2、直線和平面垂直的判定和性質(zhì);3、面面垂直的判定.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
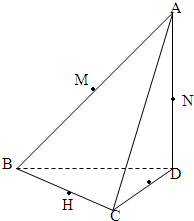 如圖所示,已知三棱錐A-BCD中,AD⊥平面BCD點(diǎn)M、N、G、H分別是棱AB、AD、DC、CB的中點(diǎn).
如圖所示,已知三棱錐A-BCD中,AD⊥平面BCD點(diǎn)M、N、G、H分別是棱AB、AD、DC、CB的中點(diǎn).| 2 |
| 6 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
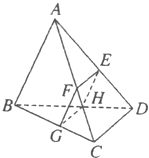 如圖所示,已知三棱錐A-BCD被一平面所截,截面為平行四邊形EFGH,求證:
如圖所示,已知三棱錐A-BCD被一平面所截,截面為平行四邊形EFGH,求證:查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
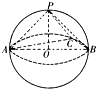 如圖所示,已知三棱錐P-ABC的各頂點(diǎn)均在一個半徑為R的球面上,球心0在AB上,P0⊥平面ABC,
如圖所示,已知三棱錐P-ABC的各頂點(diǎn)均在一個半徑為R的球面上,球心0在AB上,P0⊥平面ABC,| AB |
| BC |
| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
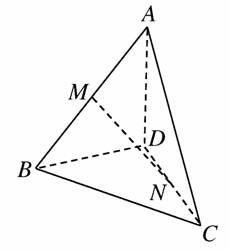
如圖所示,已知三棱錐A-BCD中M、N分別為AB、CD的中點(diǎn),則下列結(jié)論正確的是( )
A.MN≥![]() (AC+BD)
(AC+BD)
B.MN≤![]() (AC+BD)
(AC+BD)
C.MN=![]() (AC+BD)
(AC+BD)
D.MN<![]() (AC+BD)
(AC+BD)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com