Question

解不等式|x²－3x－4|＞x+1.?

Answer 1

解法一：當x＜－1時，不等式顯然成立；?

當x=－1時，不等式不成立；?

當x＞－1時，原不等式化為?

（1）或（2）

解（1）得x＞5，

解（2）得－1＜x＜3.?

故原不等式的解集為(－∞,－1)∪(－1,3)∪(5,+∞).?

解法二：原不等式等價于?

（1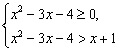）或（2）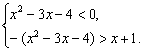

解（1）得x＜－1或x＞5,解（2）得－1＜x＜3.?

故原不等式的解集為（－∞,－1）∪（－1，3）∪（5，+∞）.

解法三：考察函數y=|x²－3x－4|和函數y=x+1的圖象：如下圖所示，由圖象可知原不等式的解為(－∞,－1)∪(－1,3)∪(5,+∞).?

點評：解法一與解法二是將原不等式轉化成等價的不等式進行求解,解法三是利用數形結合來求解.應當注意的是：在解法一和解法二中，求原不等式的解集應是兩不等式組的交集；在解法三中，應確保交點坐標準確無誤.