
 的周期為
的周期為 ,圖象的一個對稱中心為
,圖象的一個對稱中心為 ,將函數
,將函數 圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再將得到的圖象向右平移個
圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再將得到的圖象向右平移個 單位長度后得到函數
單位長度后得到函數 的圖象。
的圖象。 與
與 的解析式
的解析式 ,使得
,使得 按照某種順序成等差數列?若存在,請確定
按照某種順序成等差數列?若存在,請確定 的個數,若不存在,說明理由;
的個數,若不存在,說明理由; 與正整數
與正整數 ,使得
,使得 在
在 內恰有2013個零點
內恰有2013個零點
 (Ⅱ)存在(Ⅲ)當
(Ⅱ)存在(Ⅲ)當 ,
, 時,函數
時,函數 在
在 內恰有
內恰有 個零點
個零點 的周期為
的周期為 ,
, ,得
,得
 的一個對稱中心為
的一個對稱中心為 ,
,
 ,得
,得 ,所以
,所以
 圖象上所有點的橫坐標伸長到原來的
圖象上所有點的橫坐標伸長到原來的 倍(縱坐標不變)后可得
倍(縱坐標不變)后可得 的圖象,再將
的圖象,再將 的圖象向右平移
的圖象向右平移 個單位長度后得到函數
個單位長度后得到函數
 時,
時, ,
,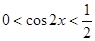

 在
在 內是否有解
內是否有解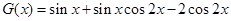 ,
,

 ,所以
,所以 ,
, 在
在 內單調遞增
內單調遞增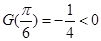 ,
,
 的圖象連續不斷,故可知函數
的圖象連續不斷,故可知函數 在
在 內存在唯一零點
內存在唯一零點 ,
, 滿足題意
滿足題意 ,令
,令
 ,即
,即 時,
時, ,從而
,從而 不是方程
不是方程 的解,所以方程
的解,所以方程 等價于關于
等價于關于 的方程
的方程 ,
,
 時方程解的情況
時方程解的情況 ,
,
 與曲線
與曲線 在
在 的交點情況
的交點情況 ,令
,令 ,得
,得 或
或
 變化時,
變化時, 和
和 變化情況如下表
變化情況如下表 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  | 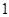 |  |  |  |  |
 且
且 趨近于
趨近于 時,
時, 趨向于
趨向于
 且
且 趨近于
趨近于 時,
時, 趨向于
趨向于
 且
且 趨近于
趨近于 時,
時, 趨向于
趨向于
 且
且 趨近于
趨近于 時,
時, 趨向于
趨向于
 時,直線
時,直線 與曲線
與曲線 在
在 內有無交點,在
內有無交點,在 內有
內有 個交點;
個交點; 時,直線
時,直線 與曲線
與曲線 在
在 內有
內有 個交點,在
個交點,在 內無交點;
內無交點; 時,直線
時,直線 與曲線
與曲線 在
在 內有
內有 個交點,在
個交點,在 內有
內有 個交點
個交點 的周期性,可知當
的周期性,可知當 時,直線
時,直線 與曲線
與曲線 在
在 內總有偶數個交點,從而不存在正整數
內總有偶數個交點,從而不存在正整數 ,使得直線
,使得直線 與曲線
與曲線 在
在 內恰有
內恰有 個交點;當
個交點;當 時,直線
時,直線 與曲線
與曲線 在
在 內有
內有 個交點,由周期性,
個交點,由周期性, ,所以
,所以
 ,
, 時,函數
時,函數 在
在 內恰有
內恰有 個零點
個零點

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:不詳 題型:單選題
 )sin(
)sin( )的單調遞增區間為( )
)的單調遞增區間為( ) | A.[(2k+1)π,2(k+1)π] | B.[(k+ )π,(k+1)π] )π,(k+1)π] |
C.[kπ,(k+ ) π] ) π] | D.[2kπ, (2k+1)π] |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
 ,給出下列命題:
,給出下列命題: 的圖象關于直線
的圖象關于直線 對稱;②函數
對稱;②函數 的圖象可由
的圖象可由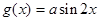 的圖象向左平移
的圖象向左平移 個單位而得到;③把函數
個單位而得到;③把函數 的圖象上的所有點的縱坐標保持不變,橫坐標縮短到原來的
的圖象上的所有點的縱坐標保持不變,橫坐標縮短到原來的 倍,可以得到函數
倍,可以得到函數 )的圖象;④若函數
)的圖象;④若函數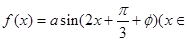 R)為偶函數,則
R)為偶函數,則 .其中正確命題的序號有 ;(把你認為正確的命題的序號都填上)。
.其中正確命題的序號有 ;(把你認為正確的命題的序號都填上)。查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com